No CrossRef data available.
Article contents
Heuristics on pairing-friendly abelian varieties
Published online by Cambridge University Press: 01 June 2015
Abstract
We discuss heuristic asymptotic formulae for the number of isogeny classes of pairing-friendly abelian varieties of fixed dimension 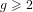 $g\geqslant 2$ over prime finite fields. In each formula, the embedding degree
$g\geqslant 2$ over prime finite fields. In each formula, the embedding degree 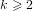 $k\geqslant 2$ is fixed and the rho-value is bounded above by a fixed real
$k\geqslant 2$ is fixed and the rho-value is bounded above by a fixed real 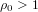 ${\it\rho}_{0}>1$ . The first formula involves families of ordinary abelian varieties whose endomorphism ring contains an order in a fixed CM-field
${\it\rho}_{0}>1$ . The first formula involves families of ordinary abelian varieties whose endomorphism ring contains an order in a fixed CM-field 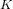 $K$ of degree
$K$ of degree  $g$ and generalizes previous work of the first author when
$g$ and generalizes previous work of the first author when 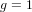 $g=1$ . It suggests that, when
$g=1$ . It suggests that, when 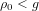 ${\it\rho}_{0}<g$ , there are only finitely many such isogeny classes. On the other hand, there should be infinitely many such isogeny classes when
${\it\rho}_{0}<g$ , there are only finitely many such isogeny classes. On the other hand, there should be infinitely many such isogeny classes when 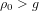 ${\it\rho}_{0}>g$ . The second formula involves families whose endomorphism ring contains an order in a fixed totally real field
${\it\rho}_{0}>g$ . The second formula involves families whose endomorphism ring contains an order in a fixed totally real field 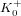 $K_{0}^{+}$ of degree
$K_{0}^{+}$ of degree  $g$ . It suggests that, when
$g$ . It suggests that, when 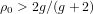 ${\it\rho}_{0}>2g/(g+2)$ (and in particular when
${\it\rho}_{0}>2g/(g+2)$ (and in particular when 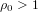 ${\it\rho}_{0}>1$ if
${\it\rho}_{0}>1$ if 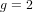 $g=2$ ), there are infinitely many isogeny classes of
$g=2$ ), there are infinitely many isogeny classes of  $g$ -dimensional abelian varieties over prime fields whose endomorphism ring contains an order of
$g$ -dimensional abelian varieties over prime fields whose endomorphism ring contains an order of 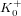 $K_{0}^{+}$ . We also discuss the impact that polynomial families of pairing-friendly abelian varieties has on our heuristics, and review the known cases where they are expected to provide more isogeny classes than predicted by our heuristic formulae.
$K_{0}^{+}$ . We also discuss the impact that polynomial families of pairing-friendly abelian varieties has on our heuristics, and review the known cases where they are expected to provide more isogeny classes than predicted by our heuristic formulae.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2015

