Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-31T08:13:03.174Z Has data issue: false hasContentIssue false
  • English
  • Français

Champ: a Cherednik algebra Magma package

Part of: Representation theory of rings and algebras Rings and algebras arising under various constructions Computational aspects of associative rings Special aspects of infinite or finite groups Permutation groups Representation theory of groups

Published online by Cambridge University Press:  01 April 2015

U. Thiel
U. Thiel*
Affiliation:
Universität Stuttgart, Fachbereich Mathematik, Pfaffenwaldring 57, 70569 Stuttgart, Germany email thiel@mathematik.uni-stuttgart.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a computer algebra package based onMagma for performing computations in rational Cherednik algebras with arbitrary parameters and in Verma modules for restricted rational Cherednik algebras. Part of this package is a new general Las Vegas algorithm for computing the head and the constituents of a module with simple head in characteristic zero, which we develop here theoretically. This algorithm is very successful when applied to Verma modules for restricted rational Cherednik algebras and it allows us to answer several questions posed by Gordon in some specific cases. We can determine the decomposition matrices of the Verma modules, the graded 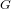$G$ -module structure of the simple modules, and the Calogero–Moser families of the generic restricted rational Cherednik algebra for around half of the exceptional complex reflection groups. In this way we can also confirm Martino’s conjecture for several exceptional complex reflection groups.

Supplementary materials are available with this article.

MSC classification

Primary: 16Z05: Computational aspects of associative rings 16G10: Representations of Artinian rings 16S38: Rings arising from non-commutative algebraic geometry
Secondary: 20B40: Computational methods 20C40: Computational methods 20F55: Reflection and Coxeter groups

Information

Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 266 - 307
Copyright
© The Author 2015 

References

Bellamy, G., ‘On singular Calogero–Moser spaces’, Bull. Lond. Math. Soc. 41 (2009) no. 2, 315–326.Google Scholar
Bellamy, G. and Martino, M., ‘On the smoothness of centres of rational Cherednik algebras in positive characteristic’, Glasg. Math. J. 55 (2011) no. A, 27–54.Google Scholar
Benard, M., ‘Schur indices and splitting fields of the unitary reflection groups’, J. Algebra 38 (1976) no. 2, 318–342.Google Scholar
Bezem, M., Klop, J. W. and de Vrijer, R., Term rewriting systems (Cambridge University Press, 2003).Google Scholar
Bonnafé, C. and Rouquier, R., ‘Cellules de Calogero–Moser’, Preprint, 2013, arXiv:1302.2720.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997) no. 3–4, 235–265.Google Scholar
Broué, M. and Kim, S., ‘Familles de caractères des algèbres de Hecke cyclotomiques’, Adv. Math. 172 (2002) no. 1, 53–136.Google Scholar
Chlouveraki, M., Blocks and families for cyclotomic Hecke algebras , Lecture Notes in Mathematics 1981 (Springer, 2009).Google Scholar
Etingof, P. and Ginzburg, V., ‘Symplectic reflection algebras, Calogero–Moser space, and deformed Harish-Chandra homomorphism’, Invent. Math. 147 (2002) no. 2, 243–348.Google Scholar
Finkelberg, M. and Ginzburg, V., ‘Calogero–Moser space and Kostka polynomials’, Adv. Math. 172 (2002) no. 1, 137–150.Google Scholar
Geck, M., An introduction to algebraic geometry and algebraic groups , Oxford Graduate Texts in Mathematics 10 (Oxford University Press, 2003).Google Scholar
Geck, M., Hiss, G., Lübeck, F., Malle, G. and Pfeiffer, G., ‘CHEVIE — a system for computing and processing generic character tables’, Appl. Algebra Engrg. Comm. Comput. 7 (1996) no. 3, 175–210; Pre-packaged GAP3 version by J. Michel (version from March 2012).Google Scholar
Geck, M. and Jacon, N., Representations of Hecke algebras at roots of unity , Algebra and Applications 15 (Springer, London, 2011).Google Scholar
Geck, M. and Pfeiffer, G., Characters of finite Coxeter groups and Iwahori–Hecke algebras , London Mathematical Society Monographs. New Series 21 (Oxford University Press, 2000).Google Scholar
Geck, M. and Rouquier, R., ‘Centers and simple modules for Iwahori–Hecke algebras’, Finite reductive groups (Luminy, 1994) , Progress in Mathematics 141 (Birkhäuser, Boston, MA, 1997) 251–272.Google Scholar
Ginzburg, V., Guay, N., Opdam, E. and Rouquier, R., ‘On the category O for rational Cherednik algebras’, Invent. Math. 154 (2003) no. 3, 617–651.Google Scholar
Gordon, I., ‘Baby Verma modules for rational Cherednik algebras’, Bull. Lond. Math. Soc. 35 (2003) 321–336.Google Scholar
Görtz, U. and Wedhorn, T., Algebraic geometry I: schemes with examples and exercises , Advanced Lectures in Mathematics (Vieweg-Teubner, Wiesbaden, 2010).Google Scholar
Holmes, R. R. and Nakano, D. K., ‘Brauer-type reciprocity for a class of graded associative algebras’, J. Algebra 144 (1991) no. 1, 117–126.Google Scholar
Holt, D. F., ‘The Meataxe as a tool in computational group theory’, The atlas of finite groups: ten years on (Birmingham, 1995) , London Mathematical Society Lecture Note Series 249 (Cambridge University Press, 1998) 74–81.Google Scholar
Holt, D. F., Eick, B. and O’Brien, E. A., Handbook of computational group theory , Discrete Mathematics and its Applications (Chapman & Hall/CRC, Boca Raton, FL, 2005).Google Scholar
Holt, D. F. and Rees, S., ‘Testing modules for irreducibility’, J. Aust. Math. Soc. Ser. A 57 (1994) no. 1, 1–16.Google Scholar
Lux, K. and Pahlings, H., Representations of groups: a computational approach , Cambridge Studies in Advanced Mathematics 124 (Cambridge University Press, Cambridge, 2010).Google Scholar
Malle, G. and Rouquier, R., ‘Familles de caractères de groupes de réflexions complexes’, Represent. Theory 7 (2003) 610–640 (electronic).Google Scholar
Martino, M., ‘The Calogero–Moser partition and Rouquier families for complex reflection groups’, J. Algebra 323 (2010) no. 1, 193–205.Google Scholar
Martino, M., ‘Blocks of restricted rational Cherednik algebras for G(m, d, n)’, J. Algebra 397 (2014) 209–224.Google Scholar
Parker, R. A., ‘The computer calculation of modular characters (the Meat-Axe)’, Computational group theory (Durham, 1982) (Academic Press, 1984) 267–274.Google Scholar
Ram, A. and Shepler, A., ‘Classification of graded Hecke algebras for complex reflection groups’, Comment. Math. Helv. 78 (2003) no. 2, 308–334.Google Scholar
Steel, A., ‘Construction of ordinary irreducible representations of finite groups’, PhD Thesis, University of Sydney, 2012.Google Scholar
Thiel, U., ‘A counter-example to Martino’s conjecture about generic Calogero–Moser families’, Algebr. Represent. Theory 17 (2014) no. 5, 1323–1348.Google Scholar
Thiel, U., ‘Decomposition matrices are generically trivial’, Preprint, 2014, arXiv:1402.5122.Google Scholar
Thiel, U., ‘On restricted rational Cherednik algebras’, Dissertation, TU Kaiserslautern, 2014.Google Scholar
Thiel, U., ‘CHAMP: a Cherednik algebra Magma package’, Preprint, 2015, arXiv:1403.6686.Google Scholar
Supplementary material: File

Thiel supplementary material

Thiel supplementary material 1

Download Thiel supplementary material(File)
File 525.6 KB