Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ahlgren, Scott
and
Andersen, Nickolas
2016.
Kloosterman Sums and Maass Cusp Forms of Half Integral Weight for the Modular Group.
International Mathematics Research Notices,
p.
rnw234.
Bykovskii, Victor Alexeevich
and
Frolenkov, Dmitry Andreevich
2017.
Асимптотические формулы для вторых моментов $L$-рядов голоморфных параболических форм на критической прямой.
Известия Российской академии наук. Серия математическая,
Vol. 81,
Issue. 2,
p.
5.
Bykovskii, V A
and
Frolenkov, D A
2017.
Asymptotic formulae for the second moments of $ L$-series of holomorphic cusp forms on the critical line.
Izvestiya: Mathematics,
Vol. 81,
Issue. 2,
p.
239.
Booker, Andrew R.
and
Then, Holger
2018.
Rapid computation of L-functions attached to Maass forms.
International Journal of Number Theory,
Vol. 14,
Issue. 05,
p.
1459.
Benson, Brian
Lakeland, Grant
and
Then, Holger
2020.
Cheeger constants of hyperbolic reflection groups and Maass cusp forms of small eigenvalues.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 1,
p.
417.
Tseng, Jimmy
2021.
Eisenstein series and an asymptotic for the K-Bessel function.
The Ramanujan Journal,
Vol. 56,
Issue. 1,
p.
323.
De Clerck, Marine
Hartnoll, Sean A.
and
Santos, Jorge E.
2024.
Mixmaster chaos in an AdS black hole interior.
Journal of High Energy Physics,
Vol. 2024,
Issue. 7,
Bian, Ce
Booker, Andrew
Docherty, Austin
Jacobson, Michael
and
Seymour-Howell, Andrei
2024.
LuCaNT: LMFDB, Computation, and Number Theory.
Vol. 796,
Issue. ,
p.
29.
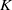 $K$-Bessel function of imaginary order
$K$-Bessel function of imaginary order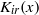 ${K}_{ir} (x)$ of imaginary order and its first two derivatives with respect to the order. We also prove precise asymptotic bounds on more general (mixed) derivatives without working out numerical implied constants. Moreover, we present an absolutely and rapidly convergent series for the computation of
${K}_{ir} (x)$ of imaginary order and its first two derivatives with respect to the order. We also prove precise asymptotic bounds on more general (mixed) derivatives without working out numerical implied constants. Moreover, we present an absolutely and rapidly convergent series for the computation of 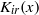 ${K}_{ir} (x)$ and its derivatives, as well as a formula based on Fourier interpolation for computing with many values of
${K}_{ir} (x)$ and its derivatives, as well as a formula based on Fourier interpolation for computing with many values of  $r$. Finally, we have implemented a subset of these features in a software library for fast and rigorous computation of
$r$. Finally, we have implemented a subset of these features in a software library for fast and rigorous computation of 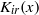 ${K}_{ir} (x)$.
${K}_{ir} (x)$.