Article contents
Amplification of filamentation instability by negative hydrogen ions stream driven by a magnetized counterstreaming e–H− plasmas
Published online by Cambridge University Press: 10 June 2015
Abstract
The main purpose of this theory is to present a simple picture of magnetic field generation by a relativistic equilibrium counterstreaming electron–negative hydrogen ion (e–H−) plasmas propagating parallel to an ambient external magnetic field. The existence of such kind of plasma flows can be imagined during the negative hydrogen ion propagation through neutralizing plasma, in order to generate an energetic neutral hydrogen beam. The produced magnetic field deflects the electron and negative hydrogen ion flows and reduces the efficiency of hydrogen neutral beam generation. We focused our analysis on the influences of the negative hydrogen ion contribution, the particles thermal velocity and the external magnetic field on the growth rate of generated sheared magnetic field. The dispersion relation is obtained using a relativistic two-fluid model and Maxwell equations. The analytical and numerical solutions admit generation of a purely growing transverse electromagnetic field across the ambient external magnetic field. It is shown that H− current filaments are responsible for deep penetration of the sheared magnetic fields into plasma, however, applying a weak magnetic field  ${\rm \omega} _{{\rm ce}}^2 {\rm \ll} {\rm \omega} _{{\rm pe}}^2 $ suppresses magnetic field generation for a counterstreaming e–H− plasma in the absence of H− ions dynamics. On the other hand, a magnetic field exists with a small growth rate for strongly magnetized (
${\rm \omega} _{{\rm ce}}^2 {\rm \ll} {\rm \omega} _{{\rm pe}}^2 $ suppresses magnetic field generation for a counterstreaming e–H− plasma in the absence of H− ions dynamics. On the other hand, a magnetic field exists with a small growth rate for strongly magnetized (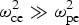 ${\rm \omega} _{{\rm ce}}^2 \;{\rm \gg}\; {\rm \omega} _{{\rm pe}}^2 $) e–H− plasma when the influence of H− ions is included. Although the growth rate is small, we expect that magnetic field generation is further amplified and the penetration depth is increased owing to H− ions stream, on a time scale much longer than the plasma period
${\rm \omega} _{{\rm ce}}^2 \;{\rm \gg}\; {\rm \omega} _{{\rm pe}}^2 $) e–H− plasma when the influence of H− ions is included. Although the growth rate is small, we expect that magnetic field generation is further amplified and the penetration depth is increased owing to H− ions stream, on a time scale much longer than the plasma period 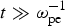 $t\;{\rm \gg}\; {\rm \omega} _{{\rm pe}}^{ - 1} $.
$t\;{\rm \gg}\; {\rm \omega} _{{\rm pe}}^{ - 1} $.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 2015
References
REFERENCES
- 2
- Cited by

