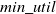1. Introduction
High utility itemset mining (HUIM) is an important sub-area of frequent itemset mining (FIM), which is the fundamental field of data mining. An itemset is frequent if that itemset possesses a frequency greater than the user-specified minimum support threshold. FIM uses the downward closure property (DCP)Footnote 1 (Agrawal & Srikant, Reference Agrawal and Srikant1994) to reduce the search-space. The FIM algorithms suffer from two major drawbacks. First, the item’s purchase quantities are not taken into account. For example, if a customer has bought two pens, five pens, or ten pens, it is viewed as the same. The second drawback is that all items have the same importance (e.g., unit profit, weight, price, etc.). For example, if a customer has bought a very expensive diamond or just an ordinary pen, it is viewed as equally important. But these assumptions often do not hold in real-life applications. In real life, retailers and corporate managers are interested in finding the itemsets that give them more profit than the items bought together frequently. Therefore, FIM does not fulfil the requirements of the user in real life. To address these important issues, the HUIM (Liu et al., Reference Liu and Liao2005; Liu & Qu, Reference Liu and Qu2012; Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014; Singh et al., Reference Singh, Shakya, Abhimanyu and Biswas2018, n.d.) field came into the limelight.
HUIM is one of the sub-fields of data mining that includes the price and quantity of items. Hence, it is an important real-life-oriented research problem in data mining. An itemset is called high utility itemsets (HUIs) if its utility value is no less than the user-specified minimum utility threshold (
![]() $min\_util$
). HUIs has many applications such as mobile commerce (Shie et al., Reference Shie, Hsiao, Tseng and Yu2011), cross-marketing analysis (Yen & Lee, Reference Yen and Lee2007
a), web usage mining (Pei et al., Reference Pei, Han, Mortazavi-Asl and Zhu2000), etc. The HUIM algorithms do not follow the DCP for support count. Hence, the FIM strategies and methods cannot be directly applied to the HUIM field. To target the issue of the DCP, Liu et al. proposed Transaction Weighted Utility (TWU)-based overestimation method (Liu et al., 2005). In the literature, there are several HUIM algorithms proposed that follow the TWU-based pruning property (Tseng et al., Reference Tseng, Wu, Shie and Yu2010, Reference Tseng, Shie, Wu and Yu2013; Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009).
$min\_util$
). HUIs has many applications such as mobile commerce (Shie et al., Reference Shie, Hsiao, Tseng and Yu2011), cross-marketing analysis (Yen & Lee, Reference Yen and Lee2007
a), web usage mining (Pei et al., Reference Pei, Han, Mortazavi-Asl and Zhu2000), etc. The HUIM algorithms do not follow the DCP for support count. Hence, the FIM strategies and methods cannot be directly applied to the HUIM field. To target the issue of the DCP, Liu et al. proposed Transaction Weighted Utility (TWU)-based overestimation method (Liu et al., 2005). In the literature, there are several HUIM algorithms proposed that follow the TWU-based pruning property (Tseng et al., Reference Tseng, Wu, Shie and Yu2010, Reference Tseng, Shie, Wu and Yu2013; Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009).
A major limitation of HUIM is setting the appropriate
![]() $min\_util$
threshold. The user does not know which value for the
$min\_util$
threshold. The user does not know which value for the
![]() $min\_util$
threshold is good for their requirements. Specifying the
$min\_util$
threshold is good for their requirements. Specifying the
![]() $min\_util$
threshold is very crucial because it directly affects the number of HUIs. If the
$min\_util$
threshold is very crucial because it directly affects the number of HUIs. If the
![]() $min\_util$
threshold is set too high, few or no HUIs are found, and we lose lots of interesting HUIs. If the
$min\_util$
threshold is set too high, few or no HUIs are found, and we lose lots of interesting HUIs. If the
![]() $min\_util$
threshold is set too low, a large number of HUIs are found. To find the appropriate
$min\_util$
threshold is set too low, a large number of HUIs are found. To find the appropriate
![]() $min\_util$
threshold, a user may thus need to run a HUIM algorithm several times. There are several top-k-based mining algorithms in the literature to solve this problem (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016; Ryang & Yun, Reference Ryang and Yun2015; Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016). In the top-k HUIM field, the value of k needs to be set instead of the
$min\_util$
threshold, a user may thus need to run a HUIM algorithm several times. There are several top-k-based mining algorithms in the literature to solve this problem (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016; Ryang & Yun, Reference Ryang and Yun2015; Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016). In the top-k HUIM field, the value of k needs to be set instead of the
![]() $min\_util$
threshold. The value of k denotes the number of itemsets the user wants to obtain. A top-k HUIM algorithm then returns the k itemsets having the highest
$min\_util$
threshold. The value of k denotes the number of itemsets the user wants to obtain. A top-k HUIM algorithm then returns the k itemsets having the highest
![]() $min\_util$
threshold. Thus, setting the value of k is much easier than
$min\_util$
threshold. Thus, setting the value of k is much easier than
![]() $min\_util$
. top-k HUIM is useful in many domains. For example, top-k HUIM is used to find the k sets of products that are the most profitable when sold together.
$min\_util$
. top-k HUIM is useful in many domains. For example, top-k HUIM is used to find the k sets of products that are the most profitable when sold together.
Top-k HUIM is a very active research area. In the literature, we find several articles based on this area, including various extensions of high utility itemset mining like closed, on-shelf, and sequential for specific needs. This paper presents a survey of top-k HUIM approaches that can serve both as an introduction and as a guide to recent advances and opportunities that will be useful for new researchers in this field.
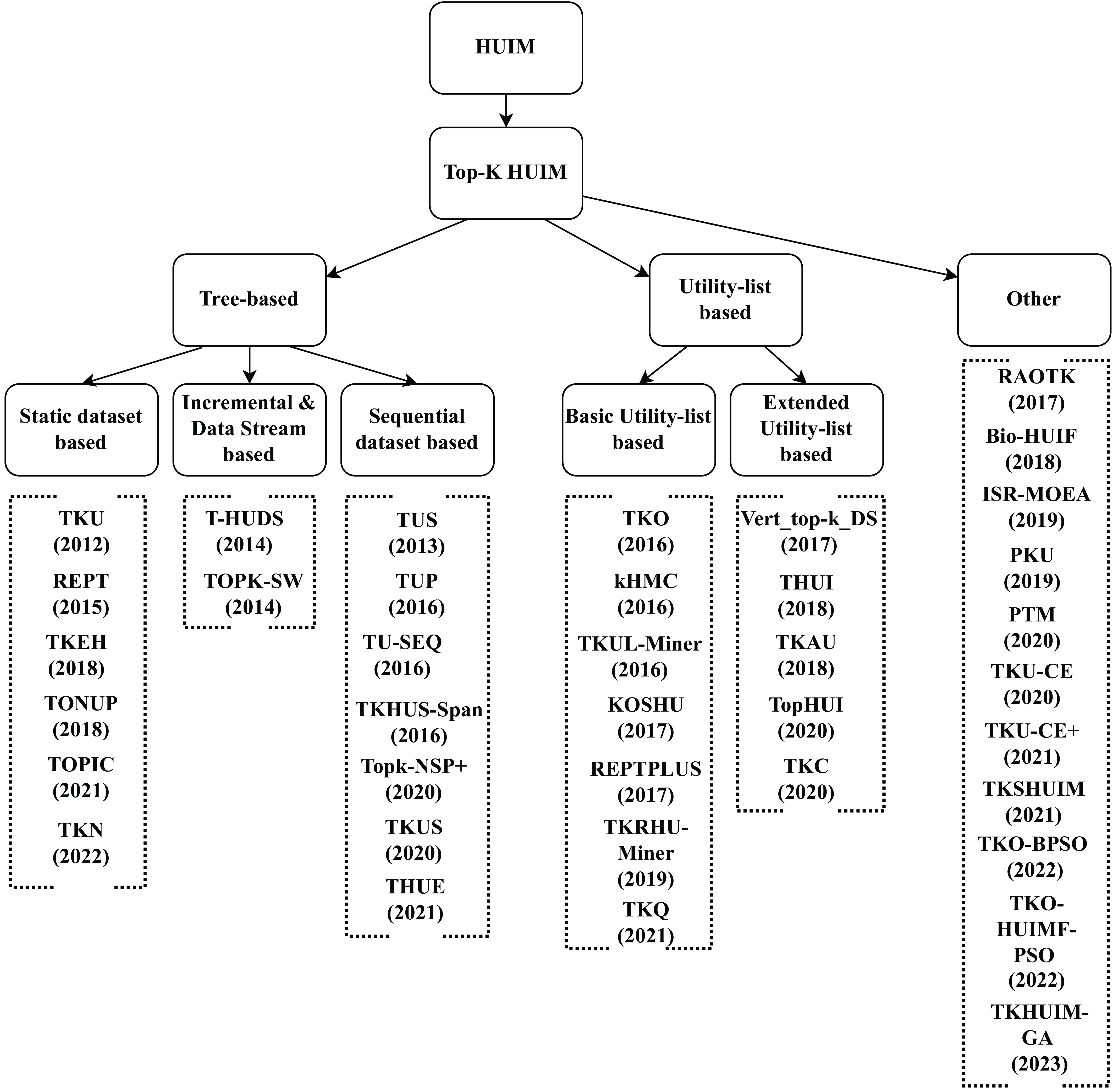
Figure 1. Taxonomy of the state-of-the-art top-k HUIM algorithms
Contribution: The present paper provides an extensive review of top-k HUIM algorithms. A taxonomy of the state-of-the-art top-k HUIM algorithms is presented in Figure 1. The major contribution of this survey is discussed below:
-
• A brief description of traditional HUIM and top-k HUIM approaches with examples is presented.
-
• A taxonomy of top-k HUIM approaches, including tree-based, utility-based, and others, is presented.
-
• A detailed comparative analysis and summary of the currently available state-of-the-art approaches are presented.
-
• The comparative advantages and disadvantages of the current state-of-the-art approaches are also demonstrated.
-
• A brief discussion and summary of the top-k HUIM approaches are presented. Furthermore, future research directions are also discussed.
Differences from existing works
In literature, some works (Zhang et al., Reference Zhang, Almpanidis, Wang and Liu2018; Rahmati & Sohrabi, Reference Rahmati and Sohrabi2019; Fournier-Viger et al., Reference Fournier-Viger, Chun-Wei Lin, Truong-Chi and Nkambou2019; Zhang et al., Reference Zhang, Han, Sun, Du and Shen2020; Gan et al., Reference Gan, Lin, Fournier-Viger, Chao, Tseng and Yu2021; Kumar & Singh, Reference Kumar and Singh2023) have been presented to discover traditional HUIs. In 2018, Zhang et al. presented an empirical evaluation survey on the HUIM algorithms. This work uses real and synthetic datasets to compare the memory usage and runtime efficiency of selected algorithms. This survey only included ten state-of-the-art HUIM algorithms. In 2019, Rahmati et al. presented a comprehensive systematic survey of HUIM approaches. This survey reviews the state-of-the-art HUIM approaches on transactional and uncertain datasets. This work compares the important properties, advantages, and drawbacks of existing approaches. The survey did not discuss any future directions for the existing HUIM field. Later, Fournier-Viger et al. (Reference Fournier-Viger, Chun-Wei Lin, Truong-Chi and Nkambou2019) presented a survey and compared the HUIM approaches. The authors classified the existing state-of-the-art approaches into two categories: one-phase and two-phase algorithms. This work highlighted little about an extension of HUIM like closed HUIs, top-k HUIs, HUIM with negative utility, HUIM with discount strategies, on-shelf HUIM, HUIs in dynamic datasets, and some other extensions. In 2020, Zhang et al. presented a survey about the key technologies for HUIM. This survey categorised the current state-of-the-art approaches into five sub-categories: Apriori-based, tree-based, projection-based, list-based, data-based, and index-based approaches. This work also discussed data-stream-based HUIM algorithms. In 2021, Gan et al. presented a structured and comprehensive survey of HUIM algorithms. The authors classified the state-of-the-art algorithms into Apriori-based, tree-based, projection-based, vertical/horizontal data-format-based, and other hybrid approaches. The survey compares the existing state-of-the-art approaches as well as shows the pros and cons of the available approaches. All the above-discussed works presented surveys only of traditional HUIM approaches. These surveys are not focused on top-k HUIM approaches.
In the literature, we found only one study that shows the comparison of transactional dataset-based top-k HUIM approaches. In 2019, Krishnamoorthy (Reference Krishnamoorthy2019 a) presented a comparative study that categorised the existing top-k HUIM algorithms into two groups: two-phase and one-phase-based algorithms. This comparative study only shows the comparison of two two-phase (TKU and REPT) and two one-phase (TKO and kHMC) algorithms. This work presents an experimental comparison among four transactional dataset-based algorithms, that is, TKU, REPT, TKU, and kHMC. The author utilized eight datasets and categorised them as sparse and dense. The experimental results include runtime performance comparisons, number of candidate-generated comparisons, and memory consumption performance comparisons. Furthermore, the author provides little discussion of other variant datasets, that is, data-stream and on-shelf-based mining approaches.
Our work is distinct from the comparative study presented by Krishnamoorthy (Reference Krishnamoorthy2019 a) on the following aspects:
• Our work presents a detailed survey of more than 35 state-of-the-art papers, whereas Krishnamoorthy’s work included only 4 papers. Our analysis included almost all the available state-of-the-art papers in the top-k HUIM field.
• Krishnamoorthy’s work is an experimental comparative study, and our work is a theoretical comparative analysis. Our analysis is more comprehensive and detailed.
• Krishnamoorthy compared only 12 internal threshold-raising strategies, whereas our analysis included more than 50 threshold-raising strategies. Our analysis discussed more than 55 pruning strategies too.
• Our analysis elaborated on the comparative advantages and disadvantages of the top-k HUIM approaches, whereas Krishnamoorthy’s study does not.
• Our taxonomy included transactional dataset-based, incremental and data-stream-based, sequential dataset-based, basic and extended utility-based, and other hybrid approaches. On the other hand, Krishnamoorthy’s study only included transactional dataset-based approaches.
• Furthermore, we discussed applications and also included a detailed summary and discussion of the top-k HUIM approaches. We also elaborated dynamic dataset-based, and both positive and negative utility value-based approaches.
Applications
User behavior mining: User behavior mining is an emerging topic in the domain of data mining. It analyses the behavior of users and has various applications, for example, website design (Pei et al., Reference Pei, Han, Mortazavi-Asl and Zhu2000), and cross-marketing analysis (Yen & Lee, Reference Yen and Lee2007 a). Periodic behavior can be defined as repeated activities at certain locations with regular time intervals (Li et al., Reference Li, Ding, Han, Kays and Nye2010). It provides insightful and concrete information about the long-moving history. The experts must have specific background knowledge in the domain that requires interesting periods or particular periods to be examined. The utility pattern mining could be used to analysis the user behavior during different time-periods. For example, physicians need to monitor older people to examine their daily and weekly behaviors.
Bio-informatics: Microarrays are effective techniques to evaluate the expression of a massive number of genes. It is used to identify the relationships between gene regulatory events and determine the biological effects of stimuli in the environment. However, it is quite a challenging task to analyse the biological effects on large-scale datasets. The utility pattern mining analysis is quite useful to identify the different genes that frequently occur in the biological conditions in the microarray dataset (Liu et al., Reference Liu, Cheng and Tseng2013). A phylogeny or phylogenetic tree is used to identify the relationship among the set of species. Utility pattern mining techniques are used to identify the common patterns, especially utility trees that are the collection of the phylogenetic tree.
Market-basket analysis: HUIM algorithms (Liu et al., Reference Liu and Liao2005) are extensively used in market-basket analysis, which is the collection of the set of items purchased by customers to generate significant profits for retail businesses, for example, Yahoo. The HUIM algorithms are quite useful for business retailers to make the correct decisions to identify highly profitable itemsets and reduce the inventory cost of more frequent but less profitable itemsets (Liu et al., Reference Liu and Liao2005).
Smart home: Due to the advancement of sensor technology, the electrical usage data of home appliances can be gathered very easily. However, the relevant information about the appliance usage data may exist but is hidden. The Correlation Pattern Miner (CoPMiner) algorithm (Chen et al., Reference Chen, Chen, Peng, Lee, Tseng, Ho, Zhou, Chen and Kao2014) is designed to identify usage patterns and correlations among appliances probabilistically. HUIM algorithms could be a promising solution to find appliance usage patterns that are useful for users to identify unnecessary appliance usage data and take corrective action for better usability of appliances. Moreover, manufacturers can better design the intelligent control system for smart appliances.
Interval-based events in temporal pattern mining: Temporal pattern mining is an interesting and important sub-field of data mining. In medical applications, temporal pattern mining identifies the frequent temporal patterns that a patient has a fever when they have a cough, and these symptoms occur when he or she has flu (Wu & Chen, Reference Wu and Chen2007). The sequential patterns identify the complex interval-based temporal relationship among events. For example, in many diabetic patients, the presence of hyperglycemia overlaps with the absence of glycosuria, which led to the development of effective diabetic testing kits. It requires identifying the complex temporal relationships among events duration. The utility pattern mining could be used to analysis the interval-based events in temporal pattern mining.
Web access pattern mining: Web access patterns are used to predict and understand the browsing behaviour of the users, which is quite useful for enhancing the user experience and website configuration. It is useful to analyse user motivation and give better recommendations and personalised services to the users. Web access patterns, also known as web navigation patterns or click-streams, represent the extracted path via one or more web pages on a website through the web server. The process of discovering patterns from web access logs is known as web usage mining (or web log mining) (Pei et al., Reference Pei, Han, Mortazavi-Asl and Zhu2000). HUIM algorithms can be quite interesting to mine the recorded information regarding the access paths of website visitors. Web access sequence (WAS) mining algorithms access the sequences of web pages visited by the users through web servers (Pei et al., Reference Pei, Han, Mortazavi-Asl and Zhu2000). It can enhance the design of a website that provides effective accessibility among highly correlated web pages, user recommendations, customer classification, and advertisement policies. HUIM algorithms are quite useful for both static and incremental mining of high-utility web access sequences.
The rest of the paper is organised as follows: Section 2 describes the key definitions and notations used in this paper. Section 3 describes the detailed discussion of top-k HUIM approaches. Section 4 presents the discussion and summary of all the available top-k HUIM approaches. Section 5 highlights the future directions for the top-k HUIM problem. Section 6 gives concluding remarks.
2. Preliminaries and definitions
Let I =
![]() $ \{ x_{1}, x_{2},\dots, x_{m} \} $
be a finite set of distinct items. A transactional dataset
$ \{ x_{1}, x_{2},\dots, x_{m} \} $
be a finite set of distinct items. A transactional dataset
![]() $D = \{T_{1}, T_2,\dots,T_n\}$
is a set of transactions, where each transaction
$D = \{T_{1}, T_2,\dots,T_n\}$
is a set of transactions, where each transaction
![]() $T_j \in D$
and n is the total number of transactions in D. Each item in the transaction has a positive integer value called the internal utility (purchase quantity) of the item. Each item
$T_j \in D$
and n is the total number of transactions in D. Each item in the transaction has a positive integer value called the internal utility (purchase quantity) of the item. Each item
![]() $I_j$
is associated with an integer value called an external utility (price or profit). If the value of external utility is not positive, then the item
$I_j$
is associated with an integer value called an external utility (price or profit). If the value of external utility is not positive, then the item
![]() $I_j$
is called a negative item.
$I_j$
is called a negative item.
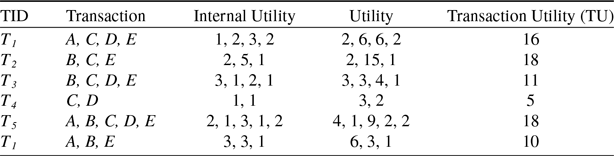
For example, Table 1 shows an example dataset containing six transactions. Each row presents the transaction, where alphabetical letters (
![]() $A, B, C, \dots$
) denote the items. Each item has its own internal utility value. Table 2 shows the external utility values for each item.
$A, B, C, \dots$
) denote the items. Each item has its own internal utility value. Table 2 shows the external utility values for each item.
Table 1. A transactional dataset

Table 2. External utility values

Definition 1
(Internal utility). Each item
![]() $x \in I $
is assigned an internal utility (purchase quantity) referred to as
$x \in I $
is assigned an internal utility (purchase quantity) referred to as
![]() $ IU(x, T_j) $
.
$ IU(x, T_j) $
.
For example, the internal utility of item A in the transaction
![]() $ T_1 $
is 1 as shown in Table 1.
$ T_1 $
is 1 as shown in Table 1.
Definition 2
(External utility). Each item
![]() $x \in I $
is assigned an external utility (e.g., unit profit) referred to as EU(x).
$x \in I $
is assigned an external utility (e.g., unit profit) referred to as EU(x).
For example, the external utility of item A is 2 as shown in Table 2.
Definition 3
(Utility of an item). The utility of an item
![]() $ x \in T_j$
is denoted by
$ x \in T_j$
is denoted by
![]() $ U(x, T_j) $
, where
$ U(x, T_j) $
, where
![]() $ U(x, T_j) $
=
$ U(x, T_j) $
=
![]() $ IU(x, T_j) $
$ IU(x, T_j) $
![]() $ \times EU(x) $
.
$ \times EU(x) $
.
For example, the utility of item A in
![]() $ T_1 $
is computed as:
$ T_1 $
is computed as:
![]() $ U(A, T_1) $
=
$ U(A, T_1) $
=
![]() $ IU (A, T_1) $
$ IU (A, T_1) $
![]() $ \times EU(A) = 1 \times 2 = 2 $
. The
$ \times EU(A) = 1 \times 2 = 2 $
. The
![]() $4^{th}$
column of Table 3 shows the utility value of each item for all the transactions.
$4^{th}$
column of Table 3 shows the utility value of each item for all the transactions.
Table 3. Transaction utility of the running example.
Definition 4
(Utility of an itemset in a transaction). The utility of an itemset X in a transaction
![]() $T_{j} (X \mathrm{\subseteq } T_{j})$
is denoted by
$T_{j} (X \mathrm{\subseteq } T_{j})$
is denoted by
![]() $U(X,T_{j})$
, which is defined as
$U(X,T_{j})$
, which is defined as
![]() $U(X,T_{j})$
=
$U(X,T_{j})$
=
![]() $\sum_{x \in X \wedge X \subseteq T_j}$
$\sum_{x \in X \wedge X \subseteq T_j}$
![]() ${U(x,T_{j})}$
.
${U(x,T_{j})}$
.
For example,
![]() $ U(\{A,C\}, T_1)$
=
$ U(\{A,C\}, T_1)$
=
![]() $ 2+ 6 = 8 $
.
$ 2+ 6 = 8 $
.
Definition 5
(Utility of an itemset in dataset). The utility of an itemset X in dataset D is denoted by U(X) which is defined as
![]() $ U(X) =\sum_{X \subseteq T_j \in D }$
$ U(X) =\sum_{X \subseteq T_j \in D }$
![]() $U(X, T_j)$
.
$U(X, T_j)$
.
For example,
![]() $ U(\{A,C\}) =$
$ U(\{A,C\}) =$
![]() $ U(\{A,C\}, T_1 ) + U(\{A,C\}, T_5) =$
$ U(\{A,C\}, T_1 ) + U(\{A,C\}, T_5) =$
![]() $ 8+13 = 21 $
.
$ 8+13 = 21 $
.
Definition 6
(Transaction utility). The transaction utility denoted by
![]() $TU (T_{j})$
, for transaction
$TU (T_{j})$
, for transaction
![]() $T_{j}$
is computed as
$T_{j}$
is computed as
![]() $ TU (T_{j}) = \sum^m_i{U(x_i, T_j)}$
, where m is the number of items in
$ TU (T_{j}) = \sum^m_i{U(x_i, T_j)}$
, where m is the number of items in
![]() $T_{j}$
transaction.
$T_{j}$
transaction.
For example,
![]() $ TU(T_1) =$
$ TU(T_1) =$
![]() $ U(A, T_1) + U(C, T_1) +$
$ U(A, T_1) + U(C, T_1) +$
![]() $ U(D, T_1) + U(E, T_1) =$
$ U(D, T_1) + U(E, T_1) =$
![]() $ 2+6+6+2=16$
. The TU of all the transactions is shown in the last column of Table 3.
$ 2+6+6+2=16$
. The TU of all the transactions is shown in the last column of Table 3.
Definition 7
(Total utility). The total utility of a dataset D is denoted as
![]() $ TU_{D} $
and is defined as
$ TU_{D} $
and is defined as
![]() $TU_{D} = \sum_{T_j \in D} TU(T_j)$
$TU_{D} = \sum_{T_j \in D} TU(T_j)$
For example, the total utility of the dataset D is
![]() $ TU_{D} =$
$ TU_{D} =$
![]() $ TU(T_1) + $
$ TU(T_1) + $
![]() $ TU(T_2) +$
$ TU(T_2) +$
![]() $ TU(T_3) +$
$ TU(T_3) +$
![]() $ TU(T_4) +$
$ TU(T_4) +$
![]() $ TU(T_5) +$
$ TU(T_5) +$
![]() $ TU(T_6) $
=
$ TU(T_6) $
=
![]() $ 16 + 18+ 11+ 5+ 18+ 10 =78$
.
$ 16 + 18+ 11+ 5+ 18+ 10 =78$
.
FIM mining discovers frequent patterns by using the DCP; however, the same support-based DCP cannot be applied to the utility value in HUIs. A low-utility itemset may become HUIs when an item is added that has a large utility value. To restore the DCP, HUIM algorithms use the TWU closure property (Liu et al., Reference Liu and Liao2005). All the HUIM algorithms follow the TWU technique to mine the HUIs (Liu et al., Reference Liu and Liao2005; Chu et al., Reference Chu, Tseng and Liang2009; Wu et al., Reference Wu, Shie, Tseng and Yu2012; Ryang & Yun, Reference Ryang and Yun2015; Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013; Zihayat & An, Reference Zihayat and An2014).
Definition 8
(Transaction-weighted utility). The transaction weighted utility of an itemset X denoted by TWU(X) can be defined as
![]() $TWU(X) =$
$TWU(X) =$
![]() $\sum_{X \subseteq T_{j} \in D} TU(T_{j})$
.
$\sum_{X \subseteq T_{j} \in D} TU(T_{j})$
.
For example,
![]() $ TWU(A) =$
$ TWU(A) =$
![]() $ TU(T_1) + TU(T_5) + TU(T_6) =$
$ TU(T_1) + TU(T_5) + TU(T_6) =$
![]() $ 16 + 18 + 10 = 44 $
. Table 4 shows the TWU values of all the items in the running example.
$ 16 + 18 + 10 = 44 $
. Table 4 shows the TWU values of all the items in the running example.
Table 4. TWU values of the running example

Property 1
(TWU based overestimation). If the TWU value of itemset X is greater than the utility value of itemset X, that is,
![]() $ TWU(X) \gt U(X) $
, then the itemset is assumed to be overestimated (Liu et al., Reference Liu and Liao2005).
$ TWU(X) \gt U(X) $
, then the itemset is assumed to be overestimated (Liu et al., Reference Liu and Liao2005).
Property 2
(TWU based search-space pruning). If the TWU value of the itemset X is less than the user-defined threshold
![]() $(min\_util) $
, that is,
$(min\_util) $
, that is,
![]() $ TWU(X) \lt min\_util $
, then the itemset cannot be included for further processing (Liu et al., Reference Liu and Liao2005).
$ TWU(X) \lt min\_util $
, then the itemset cannot be included for further processing (Liu et al., Reference Liu and Liao2005).
Definition 9
(High utility itemset). An itemset X is called a high utility itemset if the utility of itemset X is greater than or equal to the user-specified
![]() $ min\_util $
threshold, that is,
$ min\_util $
threshold, that is,
![]() $ U(X) \ge min\_util $
. Otherwise, the itemset is of low utility.
$ U(X) \ge min\_util $
. Otherwise, the itemset is of low utility.
The HUIs for running example with
![]() $ min\_util $
= 30 are as follows:
$ min\_util $
= 30 are as follows:
![]() $ \{\{A,C,D,E\}:33, \{C,D\}:35, \{C,D,E\}:35, \{B,C\}:33, \{B,C,E\}:37, \{C\}:36 $
and
$ \{\{A,C,D,E\}:33, \{C,D\}:35, \{C,D,E\}:35, \{B,C\}:33, \{B,C,E\}:37, \{C\}:36 $
and
![]() $ \{C,E\}:39\}$
, where the number beside each itemset indicates its utility value.
$ \{C,E\}:39\}$
, where the number beside each itemset indicates its utility value.
Definition 10 (Closed itemset). An itemset X is a closed itemset if there is no super-set of itemset X with the same support count. Otherwise, the itemset X is a non-closed itemset.
Two-phase-based algorithms suffer from multiple dataset scans and the generation of lots of candidates. To overcome these limitations, we found several proposed one-phase algorithms. One-phase algorithms are more efficient than two-phase algorithms in terms of execution time and memory space. Most of the one-phase algorithms use a utility-list-based data structure to store information about items, and the remaining utility-based pruning strategy to prune the search-space (Liu & Qu, Reference Liu and Qu2012).
Definition 11
(Remaining utility of an itemset in a transaction). The remaining utility of itemset X in transaction
![]() $ T_j $
denoted by
$ T_j $
denoted by
![]() $ RU(X, T_j) $
is the sum of the utilities of all the items in
$ RU(X, T_j) $
is the sum of the utilities of all the items in
![]() $ T_j/X $
in
$ T_j/X $
in
![]() $ T_j $
where
$ T_j $
where
![]() $ RU(X, T_j) $
=
$ RU(X, T_j) $
=
![]() $ \sum_{i \in (T_j /X)} $
U(i, T) (Liu & Qu, Reference Liu and Qu2012).
$ \sum_{i \in (T_j /X)} $
U(i, T) (Liu & Qu, Reference Liu and Qu2012).
Definition 12
(Utility-list structure). The utility-list structure contains three fields,
![]() $ T_{id}, iutil,$
and rutil. The
$ T_{id}, iutil,$
and rutil. The
![]() $ T_{id} $
indicates the transactions containing itemset X, iutil indicates the U(X), and the rutil indicates the remaining utility of itemset X is
$ T_{id} $
indicates the transactions containing itemset X, iutil indicates the U(X), and the rutil indicates the remaining utility of itemset X is
![]() $RU(X,T_j)$
(Liu & Qu, Reference Liu and Qu2012).
$RU(X,T_j)$
(Liu & Qu, Reference Liu and Qu2012).
Property 3
(Pruning search-space using remaining utility). For an itemset X, if the sum of
![]() $ U(X)+RU(X) $
is less than
$ U(X)+RU(X) $
is less than
![]() $min\_util $
, then itemset X and all its supersets are low utility itemsets. Otherwise, the itemset is eligible for HUIs. The details and proof of the remaining utility upper-bound (REU)-based upper-bound are given in Liu and Qu (Reference Liu and Qu2012).
$min\_util $
, then itemset X and all its supersets are low utility itemsets. Otherwise, the itemset is eligible for HUIs. The details and proof of the remaining utility upper-bound (REU)-based upper-bound are given in Liu and Qu (Reference Liu and Qu2012).
Definition 13 (top-k high utility itemset). An itemset X is top-k HUIs if there exist no more than (k-1) itemsets whose utility is higher than that of X.
In the running example, Table 5 shows the HUIs for k, where the value of k is 10.
Table 5. High utility itemsets where
![]() $ k=10 $
$ k=10 $

3. Top-k high utility itemset mining algorithms
HUIM algorithms (Tseng et al., Reference Tseng, Wu, Shie and Yu2010; Liu & Qu, Reference Liu and Qu2012; Tseng et al., Reference Tseng, Shie, Wu and Yu2013) are proposed that consider both users’ preferences and items’ importance (for example, weight, cost, profit, quantity, and others). However, HUIM does not follow the anti-monotonic property (Liu et al., Reference Liu and Liao2005; Agrawal & Srikant, Reference Agrawal and Srikant1994). To deal with this issue, most of the HUIM approaches (Liu et al., Reference Liu and Liao2005; Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009) adopt the TWU model (Liu et al., Reference Liu and Liao2005) that follows the TWDCP (Transaction-Weighted Downward Closure Property)Footnote 2 . However, traditional HUIM approaches suffer from the following drawbacks: (1) generation of numerous unpromising candidate itemsets. (2) scanning the dataset multiple times. (3) It is difficult to set the appropriate threshold in advance. To address these issues, we discuss the top-k HUIM algorithms in-depth that solve the above problems to a large extent. We divide the top-k HUIM into three parts, namely tree-based, utility-list-based, and others.
3.1 Tree-based top-k HUIM algorithms
Tree-based top-k HUIM algorithms are categorised into the following three broad areas of datasets: (1) static, (2) incremental and data stream, and (3) sequential.
3.1.1 Static dataset-based algorithms
Top-k HUIM algorithms (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Ryang & Yun, Reference Ryang and Yun2015) are designed to mine top-k HUIs where the user can specify the value of k to obtain the intended itemsets. It is easy to set the value of k instead of setting the
![]() $min\_util$
threshold. However, it incurs the following challenges: (1) The utility value of the itemsets is neither monotone nor anti-monotone. (2) Present a novel data structure to store the items. (3) It is difficult to raise the intermediate threshold from 0 to prune the search-space. In this sub-section, we have provided the most up-to-date discussion about the static dataset-based top-k HUIM algorithms.
$min\_util$
threshold. However, it incurs the following challenges: (1) The utility value of the itemsets is neither monotone nor anti-monotone. (2) Present a novel data structure to store the items. (3) It is difficult to raise the intermediate threshold from 0 to prune the search-space. In this sub-section, we have provided the most up-to-date discussion about the static dataset-based top-k HUIM algorithms.
Wu et al. (Reference Wu, Shie, Tseng and Yu2012) developed an effective approach, named TKU (Top-K Utility itemset mining), to discover all the HUIs without setting a minimum-utility threshold from the transactional dataset. Firstly, the authors present a baseline algorithm, named TKU
![]() $_{Base}$
, an extension of UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) and adopt the UP-Tree (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), to keep the details of transactions and top-k HUIs. TKU
$_{Base}$
, an extension of UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) and adopt the UP-Tree (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), to keep the details of transactions and top-k HUIs. TKU
![]() $_{Base}$
consists of the following three parts: (1) constructs the UP-Tree as in Tseng et al. (Reference Tseng, Wu, Shie and Yu2010) and requires two dataset scans, (2) generates the Potential top-k HUIs (PKHUIs) from the UP-Tree, and (3) identifies the actual top-k HUIs from the set of PKHUIs. Four threshold-raising strategies, namely, raising the threshold by Minimum-Utility Itemsets (MUI) of Candidate (MC), Pre-Evaluation (PE), raising the threshold by Node Utilities (NU), and raising the threshold by MIU of Descendants (MD), are designed. The MC strategy is used to determine that the estimated utility is no less than the border threshold. The PE strategy raises the border threshold after the first scan by using the Pre-evaluation Matrix (PEM) structure, which keeps the lower bounds of utility for the particular 2-itemsets. During the second dataset scan, the NU strategy is performed while constructing the UP-Tree. The MD strategy is performed after UP-Tree construction and before PKHUIs generation. These strategies effectively reduce the search-space and unpromising candidates in the first phase. As the number of checked PKHUIs is too high, it takes a lot of time to scan the dataset. To mitigate this effect in the second phase, the fifth threshold-raising strategy, named Sorting candidates and raising threshold by the Exact utility of candidates (SE), is designed to enhance the mining performance by minimising the number of checked candidates. Three versions of TKU, namely TKU, TKU
$_{Base}$
consists of the following three parts: (1) constructs the UP-Tree as in Tseng et al. (Reference Tseng, Wu, Shie and Yu2010) and requires two dataset scans, (2) generates the Potential top-k HUIs (PKHUIs) from the UP-Tree, and (3) identifies the actual top-k HUIs from the set of PKHUIs. Four threshold-raising strategies, namely, raising the threshold by Minimum-Utility Itemsets (MUI) of Candidate (MC), Pre-Evaluation (PE), raising the threshold by Node Utilities (NU), and raising the threshold by MIU of Descendants (MD), are designed. The MC strategy is used to determine that the estimated utility is no less than the border threshold. The PE strategy raises the border threshold after the first scan by using the Pre-evaluation Matrix (PEM) structure, which keeps the lower bounds of utility for the particular 2-itemsets. During the second dataset scan, the NU strategy is performed while constructing the UP-Tree. The MD strategy is performed after UP-Tree construction and before PKHUIs generation. These strategies effectively reduce the search-space and unpromising candidates in the first phase. As the number of checked PKHUIs is too high, it takes a lot of time to scan the dataset. To mitigate this effect in the second phase, the fifth threshold-raising strategy, named Sorting candidates and raising threshold by the Exact utility of candidates (SE), is designed to enhance the mining performance by minimising the number of checked candidates. Three versions of TKU, namely TKU, TKU
![]() $_{noSE}$
, and TKU
$_{noSE}$
, and TKU
![]() $_{Base}$
, are proposed to measure the effectiveness of the developed strategies that are shown in Table 6.
$_{Base}$
, are proposed to measure the effectiveness of the developed strategies that are shown in Table 6.
Table 6. Comparison of three designed versions of the TKU by using different threshold-raising strategies (Wu et al., Reference Wu, Shie, Tseng and Yu2012)

The experimental results show that TKU performs better than TKU
![]() $_{Base}$
and is close to the optimal case of UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) for the execution time over the foodmart, mushroom and chain-store datasets. It is observed that the execution time of TKU is up-to 100 times faster than that of TKU
$_{Base}$
and is close to the optimal case of UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) for the execution time over the foodmart, mushroom and chain-store datasets. It is observed that the execution time of TKU is up-to 100 times faster than that of TKU
![]() $_{Base}$
and two times less than the optimal case of UP-Growth. However, TKU relies on a two-phase model, thereby resulting in a large number of candidates and multiple dataset scans.
$_{Base}$
and two times less than the optimal case of UP-Growth. However, TKU relies on a two-phase model, thereby resulting in a large number of candidates and multiple dataset scans.
TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) fails to process all the patterns having utilities that are less than the specified threshold. To resolve this issue, Ryang and Yun (Reference Ryang and Yun2015) developed an effective approach, named REPT (Raising threshold with Exact and Pre-calculated utilities for Top-k high utility pattern mining), to find the top-k HUIs with highly reduced candidates from the non-binary datasets. Three threshold-raising strategies, namely, raising the threshold based on Pre-evaluation with Utility Descending order (PUD), raising the threshold by Real Item Utilities (RIU), and Raising the threshold with items in Support Descending order (RSD), are designed with exact and pre-evaluated utility of itemsets of length 1 or 2 in the first phase. During the second phase, the fourth threshold-raising strategy, named Sorting candidates and raising the threshold Exact and Pre-calculated utilities of candidates (SEP), is designed with exact and pre-calculated utilities to identify the actual top-k HUIs. The primary differences between REPT and TKU are as follows: (1) During the first dataset scan, TKU employs the PE strategy, based on only pre-evaluated itemsets, while REPT employs two strategies, PUD and RIU, based on both exact and pre-evaluated itemsets. (2) During the second dataset scan, TKU constructs the tree using MD and NU strategies, while REPT increases the threshold again by using RSD and NU strategies. (3) TKU uses the SE strategy to employ only upper-bound utilities, while REPT uses the SEP strategy to employ both exact and pre-calculated utilities of itemsets. Therefore, REPT significantly performs better than TKU. The difference between REPT and TKU for the different threshold-raising strategies is shown in Table 7.
Table 7. Threshold-raising strategies used by REPT and TKU (Ryang & Yun, Reference Ryang and Yun2015)

It is observed that REPT performs better compared to the state-of-the-art works TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and the optimal case of UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) and UP-Growth
![]() $^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013) for the number of generated candidates, runtime, memory utilisation, and scalability from the dense and sparse datasets. Moreover, REPT effectively raises the threshold as compared to the TKU algorithm (Wu et al., Reference Wu, Shie, Tseng and Yu2012) for different values of k and N (where N denotes the number of items). However, REPT incurs the same drawbacks as the TKU approach. Furthermore, it is a tedious job for the users to specify the suitable values of N, used by the RSD strategy.
$^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013) for the number of generated candidates, runtime, memory utilisation, and scalability from the dense and sparse datasets. Moreover, REPT effectively raises the threshold as compared to the TKU algorithm (Wu et al., Reference Wu, Shie, Tseng and Yu2012) for different values of k and N (where N denotes the number of items). However, REPT incurs the same drawbacks as the TKU approach. Furthermore, it is a tedious job for the users to specify the suitable values of N, used by the RSD strategy.
REPT and TKU follow the two-phase model; therefore, these algorithms generate excessive candidates and perform multiple dataset scans to find the accurate utilities of itemsets and extract the desired top-k HUIs. To address these issues, Singh et al. (Reference Singh, Singh, Kumar and Biswas2019b) developed an effective method, named TKEH (Efficient algorithm for mining top-k high utility itemsets), to find the top-k HUIs from the transactional datasets. TKEH adopts the Estimated Utility Co-occurrence Pruning Strategy with Threshold (EUCST), an extended version of FHM (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014) and later improved by kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016). EUCST efficiently raises the minimum utility threshold to prune the search-space. The EUCS structure is implemented using a hash map instead of a triangular matrix, as in Fournier-Viger et al. (Reference Fournier-Viger, Wu, Zida and Tseng2014). TKEH scans the dataset twice. In the first dataset scan, it computes the TWU of each 1-item and sorts items as per the increasing order of TWU, while during the second scan, it builds the EUCS structure. However, it is very costly to scan the dataset. To mitigate this effect, the proposed algorithm adopts database projection and transaction merging techniques from EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015). Both of these techniques effectively reduce the dataset size, thereby resulting in high cost-effectiveness of the dataset scans. However, the transaction merging technique finds lots of identical transactions. To implement these techniques efficiently, TKEH adopts the method as used in EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015). The proposed work adopts the following three threshold-raising strategies: (1) The first strategy, Real Time Utilities (RIU), is adopted from REPT (Ryang & Yun, Reference Ryang and Yun2015), and it raises the minimum utility to the
![]() $k{\rm th} $
largest value stored in the RIU list. (2) Second strategy: CUD is adopted from kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), and it incorporates the EUCS structure to keep the utilities of 2-itemsets. CUD is applied after the RIU strategy. (3) The third strategy, Coverage (COV), is used to store the pairs of items in the Coverage List (COVL) structure. Two pruning strategies, namely Pruning using sub-tree (SUP) and Pruning using EUC (EUCP), are incorporated to efficiently reduce the search-space. SUP uses the notion of sub-tree utility as in Zida et al. (Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015), while EUCP is used to get the TWU value of each itemset using the EUCS structure.
$k{\rm th} $
largest value stored in the RIU list. (2) Second strategy: CUD is adopted from kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), and it incorporates the EUCS structure to keep the utilities of 2-itemsets. CUD is applied after the RIU strategy. (3) The third strategy, Coverage (COV), is used to store the pairs of items in the Coverage List (COVL) structure. Two pruning strategies, namely Pruning using sub-tree (SUP) and Pruning using EUC (EUCP), are incorporated to efficiently reduce the search-space. SUP uses the notion of sub-tree utility as in Zida et al. (Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015), while EUCP is used to get the TWU value of each itemset using the EUCS structure.
To measure the effectiveness of the strategies used, five versions of TKEH are designed, namely TKEH, TKEH(CUD), TKEH(RIU), TKEH(sup), and TKEH(tm). Experiments show that TKEH with five versions performs better in contrast to the state-of-the-art TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), and kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) for runtime, memory utilisation, and scalability in dense and sparse datasets. The proposed algorithm is 2.66 times and 73.98 times faster than that of kHMC and TKO, respectively, for k = 1000. On the other side, TKU does not work for k = 1000. However, TKEH shows poor performance on highly sparse datasets, for example, the retail dataset. The reason is that the proposed algorithm does not utilise transaction merging and database projection techniques properly for the highly sparse datasets.
Liu et al. (Reference Liu, Zhang, Fung, Li and Iqbal2018) proposed a novel one-phase, efficient and scalable algorithm, named TONUP (TOp-N high Utility Pattern mining), an extension of d
![]() $^2$
HUP (Liu et al., Reference Liu, Wang and Fung2016) and formulated upon the opportunistic pattern-growth approach, to mine the long top-n HUPs without generating candidates. It grows top-k HUPs by enumerating patterns as prefix extensions using depth-first search, computes the utility of each enumerated pattern by using an improved memory-resident structure, shortlists patterns with the first n larger utilities among the enumerate patterns, and employs the
$^2$
HUP (Liu et al., Reference Liu, Wang and Fung2016) and formulated upon the opportunistic pattern-growth approach, to mine the long top-n HUPs without generating candidates. It grows top-k HUPs by enumerating patterns as prefix extensions using depth-first search, computes the utility of each enumerated pattern by using an improved memory-resident structure, shortlists patterns with the first n larger utilities among the enumerate patterns, and employs the
![]() $n{\rm th}$
largest utility as a border threshold to prune the search-space. The memory-resident data structure, improved Chain of Accurate Utility Lists (iCAUL), an extended version of CAUL (Liu et al., Reference Liu, Wang and Fung2016), is proposed to store the utilities of enumerated patterns to enhance the mining performance. Materialized projection is efficient to eliminate the unpromising items by enumerating the prefix extensions, but it incurs additional overhead to allocate the memory and copy transactions. Therefore, a materialize transaction set for patterns is selected based on the pattern length and the percentage of promising items. On the other hand, pseudo-projection is independent of data characteristics, removing the burden on users. Materialized projection works well on dense datasets, while pseudo-projection works well on sparse datasets. The Automatic Materialization in projecting TS (AutoMaterial) strategy provides a balance between pseudo- and materialized projection of transaction sets, maintained in iCAUL by using the self-adjusting method. The Dynamically resorting items in DESCENDing order (DynaDescend) strategy is used to initialise and dynamically adjust the border threshold and dynamically resort the items in the decreasing order of local utility upper-bound. However, it incurs additional costs to dynamically resort to the items. An opportunistic strategy is proposed that maintains the shortlisted patterns, efficiently computes the utilities, quickly raises the border threshold, handles the very long patterns, and captures every opportunity to enhance the efficiency and scalability of full-strength TONUP. The full-strength TONUP uses a suffix tree to keep and shortlist the enumerated patterns. The threshold-raising strategy, named Exact utilities to raise a Border threshold (ExactBoarder), is incorporated to rapidly raise the border threshold by the exact utility of each enumerated pattern using min-heap. The threshold-raising strategy, named Suffix Tree to maintain patterns (SuffixTree), is incorporated to efficiently keep the shortlisted patterns by using a suffix tree. The Opportunistic Shift to a two-round approach (OppoShift) strategy opportunistically shifts the two-round method when the enumerated patterns are too long. The two-round TONUP is up to three times faster than the one-round TONUP.
$n{\rm th}$
largest utility as a border threshold to prune the search-space. The memory-resident data structure, improved Chain of Accurate Utility Lists (iCAUL), an extended version of CAUL (Liu et al., Reference Liu, Wang and Fung2016), is proposed to store the utilities of enumerated patterns to enhance the mining performance. Materialized projection is efficient to eliminate the unpromising items by enumerating the prefix extensions, but it incurs additional overhead to allocate the memory and copy transactions. Therefore, a materialize transaction set for patterns is selected based on the pattern length and the percentage of promising items. On the other hand, pseudo-projection is independent of data characteristics, removing the burden on users. Materialized projection works well on dense datasets, while pseudo-projection works well on sparse datasets. The Automatic Materialization in projecting TS (AutoMaterial) strategy provides a balance between pseudo- and materialized projection of transaction sets, maintained in iCAUL by using the self-adjusting method. The Dynamically resorting items in DESCENDing order (DynaDescend) strategy is used to initialise and dynamically adjust the border threshold and dynamically resort the items in the decreasing order of local utility upper-bound. However, it incurs additional costs to dynamically resort to the items. An opportunistic strategy is proposed that maintains the shortlisted patterns, efficiently computes the utilities, quickly raises the border threshold, handles the very long patterns, and captures every opportunity to enhance the efficiency and scalability of full-strength TONUP. The full-strength TONUP uses a suffix tree to keep and shortlist the enumerated patterns. The threshold-raising strategy, named Exact utilities to raise a Border threshold (ExactBoarder), is incorporated to rapidly raise the border threshold by the exact utility of each enumerated pattern using min-heap. The threshold-raising strategy, named Suffix Tree to maintain patterns (SuffixTree), is incorporated to efficiently keep the shortlisted patterns by using a suffix tree. The Opportunistic Shift to a two-round approach (OppoShift) strategy opportunistically shifts the two-round method when the enumerated patterns are too long. The two-round TONUP is up to three times faster than the one-round TONUP.
TONUP is 1 to 3 orders of magnitude more efficient than the benchmark algorithms, TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), and up to 2 orders of magnitude faster than the optimal case of the state-of-the-art methods, UP-Growth
![]() $^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013), HUI-Miner (Liu & Qu, Reference Liu and Qu2012) and EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015). The proposed algorithm incurs several disadvantages. It works only for static datasets. Therefore, an incremental algorithm may be used to discover top-n HUPs from dynamic datasets. The proposed algorithm only considers small and medium-sized datasets that can be entirely kept in memory. In cases of massive data that cannot be completely occupied in memory, it fails to discover top-k HUIs directly. One probable solution is that firstly, an extension is utilised to retrieve the data from datasets subject to memory constraints, then computes the local top-k HUIs, and finally fetches results from local datasets. However, this process is cumbersome, generates lots of unpromising candidates, and degrades mining performance.
$^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013), HUI-Miner (Liu & Qu, Reference Liu and Qu2012) and EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015). The proposed algorithm incurs several disadvantages. It works only for static datasets. Therefore, an incremental algorithm may be used to discover top-n HUPs from dynamic datasets. The proposed algorithm only considers small and medium-sized datasets that can be entirely kept in memory. In cases of massive data that cannot be completely occupied in memory, it fails to discover top-k HUIs directly. One probable solution is that firstly, an extension is utilised to retrieve the data from datasets subject to memory constraints, then computes the local top-k HUIs, and finally fetches results from local datasets. However, this process is cumbersome, generates lots of unpromising candidates, and degrades mining performance.
TopHUI (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) is the first work that can mine top-k HUIs with or without negative utility; however, it incurs high memory costs and a long runtime. To resolve these problems, Chen et al. (Reference Chen, Wan, Gan, Chen and Fujita2021) proposed an approach named TOPIC (TOP-k high utility Itemset disCovering), with positive and negative utility from the large dataset. An array-based utility-counting method is adopted to efficiently compute the utility bounds to minimise the unpromising candidate generations. Two novel upper bounds, namely Redefined Local Utility and Redefined Sub-tree Utility, are utilised by using the utility-array (UA) to quickly reduce the search-space. TOPIC is an extension of EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015), and traverses the search-space by adopting the depth-first method. The items are arranged according to the increasing order of TWU in the search-space when there are only positive utility values. However, in the case of negative utility values, the ascending order of RTWU is considered to follow the lexicographical order. The negative items always follow the positive items in sorted order. The proposed approach incorporates two efficient dataset scanning techniques, namely transaction merging and dataset projection, to minimise the dataset scan cost and memory usage. Two pruning strategies, namely TWU-based pruning strategy (Liu t al., 2005) and RTWU-based pruning strategy (Fournier-Viger, Reference Fournier-Viger, Luo, Yu and Li2014), are adopted to effectively reduce the search-space and discover the exact top-k HUIs. The Priority-queue and threshold-raising strategy, RIU (Ryang & Yun, Reference Ryang and Yun2015), are employed, respectively, to store the itemsets and automatically raise the minimum-utility threshold.
Four versions of the proposed algorithm, namely TOPIC
![]() $_{merge}$
, TOPIC
$_{merge}$
, TOPIC
![]() $_{sub-tree}$
, TOPIC, and TOPIC
$_{sub-tree}$
, TOPIC, and TOPIC
![]() $_{none}$
, are designed to evaluate the effectiveness of adopted strategies. Experiments show that TOPIC outperforms the other proposed versions. The reason is that TOPIC does not require keeping unnecessary details in memory. TOPIC works better than the state-of-the-art TopHUI (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) concerning the runtime, memory cost, and scalability on the benchmark datasets. It produces excellent performance on dense and moderately dense datasets. TOPIC adopts an efficient data structure to avoid the large amount of information stored in memory, thereby resulting in high performance. Moreover, the versions of the proposed algorithm, TOPIC
$_{none}$
, are designed to evaluate the effectiveness of adopted strategies. Experiments show that TOPIC outperforms the other proposed versions. The reason is that TOPIC does not require keeping unnecessary details in memory. TOPIC works better than the state-of-the-art TopHUI (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) concerning the runtime, memory cost, and scalability on the benchmark datasets. It produces excellent performance on dense and moderately dense datasets. TOPIC adopts an efficient data structure to avoid the large amount of information stored in memory, thereby resulting in high performance. Moreover, the versions of the proposed algorithm, TOPIC
![]() $_{merge}$
, TOPIC
$_{merge}$
, TOPIC
![]() $_{sub-tree}$
, and TOPIC
$_{sub-tree}$
, and TOPIC
![]() $_{none}$
, are significantly better than TopHUI because of the adoption of tight upper bounds for RSU and RLU. It is observed that the proposed algorithm is up to 3, 20, 4, and 2 times faster as compared to TopHUI (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) on the Retail, Chess, Mushroom, and T10I4D100K datasets, respectively. Furthermore, TOPIC consumes 8 times less memory than TopHUI to complete the mining process. However, more efficient threshold auto-raising strategies and compressed data structures can be designed for high mining performance.
$_{none}$
, are significantly better than TopHUI because of the adoption of tight upper bounds for RSU and RLU. It is observed that the proposed algorithm is up to 3, 20, 4, and 2 times faster as compared to TopHUI (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) on the Retail, Chess, Mushroom, and T10I4D100K datasets, respectively. Furthermore, TOPIC consumes 8 times less memory than TopHUI to complete the mining process. However, more efficient threshold auto-raising strategies and compressed data structures can be designed for high mining performance.
There are some top-k HUIM algorithms (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020; Chen et al., Reference Chen, Wan, Gan, Chen and Fujita2021) available in the literature that deal with the negative itemsets. However, they are not performed well in terms of runtime, memory consumption, weak pattern pruning, and scalability. To deal with these issues, Ashraf et al. (Reference Ashraf, Abdelkader, Rady and Gharib2022) proposed an efficient generalised and adaptive algorithm, named TKN (Efficiently mining Top-K HUIs with positive or Negative profits), to mine top-k HUIs from the positive and negative profit datasets. It uses the pattern-growth method that eliminates the unpromising candidates that exist in the dataset by using a depth-first search. It uses a horizontal dataset presentation as used in EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015) that merges the duplicate transactions in the projected datasets, which significantly improves the mining performance. The proposed algorithm utilised transaction projection and merging techniques to significantly reduce the visiting cost of the dataset, thereby significantly reducing execution time and memory usage. A data structure, named LIU, is adopted from THUI (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021) that keeps the utilities of itemsets in an ordered way in compact form. It is used to efficiently raise the minimum utility threshold while holding both positive and negative utility. An upper-bound PTWU is introduced to reduce the number of possible HUIs. Another upper-bound Remaining Utility (REU) is adopted from HUI-Miner (Liu & Qu, Reference Liu and Qu2012) to narrow the search-space of the mining process. Two efficient pruning properties, namely Positive sub-tree utility (PSU) and Positive local utility (PLU) are used to prune the search-space in a depth-first search manner. PSU and PLU are the generalised versions of the sub-tree utility and local utility as proposed in EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015). Two novel pruning strategies, namely Early pruning (EP) and Early abandoning (EA), are designed. The EP strategy reduces the computational cost of constructing the projected datasets of the prefix itemsets. The EA strategy reduces the number of evaluations to estimate the upper-bound PSU and PLU of the candidates without performing unnecessary dataset scans, thereby increasing mining speed. An array-based approach is utilised to compute the utility and upper bounds in linear time, thus achieving the maximum efficiency to estimate the utility of itemsets. There are three threshold-raising strategies, namely Positive real item utility (PRIU), Positive LIU-Exact (PLIU_E), and Positive LIU-Lower Bound (PLIU_LB), to effectively raise the minimum utility threshold. PRIU strategy is the generalised version of RIU strategy, adopted from the REPT algorithm (Ryang & Yun, Reference Ryang and Yun2015) that is used to raise the minimum utility threshold from the zero value during the first scan. PLIU_E strategy is based on the LIU-E strategy to raise the minimum utility threshold stored in the LIU structure by using the priority queue PIQU_LIU of size k. The PLIU_LB strategy is based on LIU-LB (Krishnamoorthy, Reference Krishnamoorthy2019 b) that computes the lower-bound utility for each stored sequence in the LIU structure.
Three variants of the proposed algorithm, namely TKN(PRIU), TKN(PSU), and TKN(TM) are developed to measure the effectiveness of TKN. TKN(PRIU), TKN(PSU), and TKN(TM) use all the techniques except LIUS-based strategies, transaction merging techniques, and PSU pruning strategies, respectively. It is observed that TKN achieves high speed as compared to TKN(PRIU), TKN(PSU), and TKN(TM). The performance of the proposed algorithm is compared against the negative top-k HUIM, named THN (Sun et al., Reference Sun, Han, Zhang, Shen and Du2021), top-k HUIM, namely THUI (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021) and TKEH (Singh et al., Reference Singh, Singh, Kumar and Biswas2019b), and finally with the optimal case of negative-utility-based HUIM, namely FHN (Fournier-Viger, Reference Fournier-Viger, Luo, Yu and Li2014) and GHUM (Krishnamoorthy, Reference Krishnamoorthy2018), in terms of execution time and memory consumption from the dense and sparse datasets. The experimental results show that TKN achieves one order of magnitude more efficiently than THN and about four orders of magnitude more efficiently than THUI and TKEH on highly dense and large datasets. TKN obtains performance very close to the optimal cases of FHN and GHUM. It is observed that for different values of k, TKN prunes 82 percent at the early stages, which saves a significant amount of time. TKN reduces the number of evaluations by 28 percent by computing the upper bound using the EA strategy.
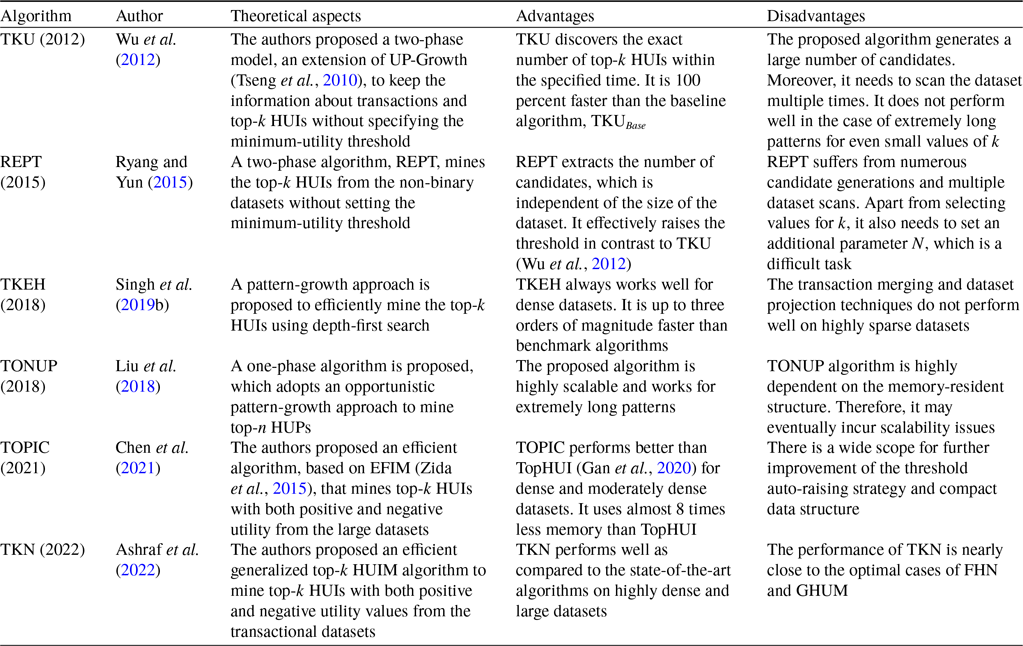
Table 8 describes the overview of the tree-based top-k HUIM algorithms for static datasets. Table 9 highlights the pros and cons of all the available state-of-the-art tree-based top-k HUIM algorithms for static datasets.
Table 8. An overview of the tree-based top-k HUIM algorithms for the static datasets
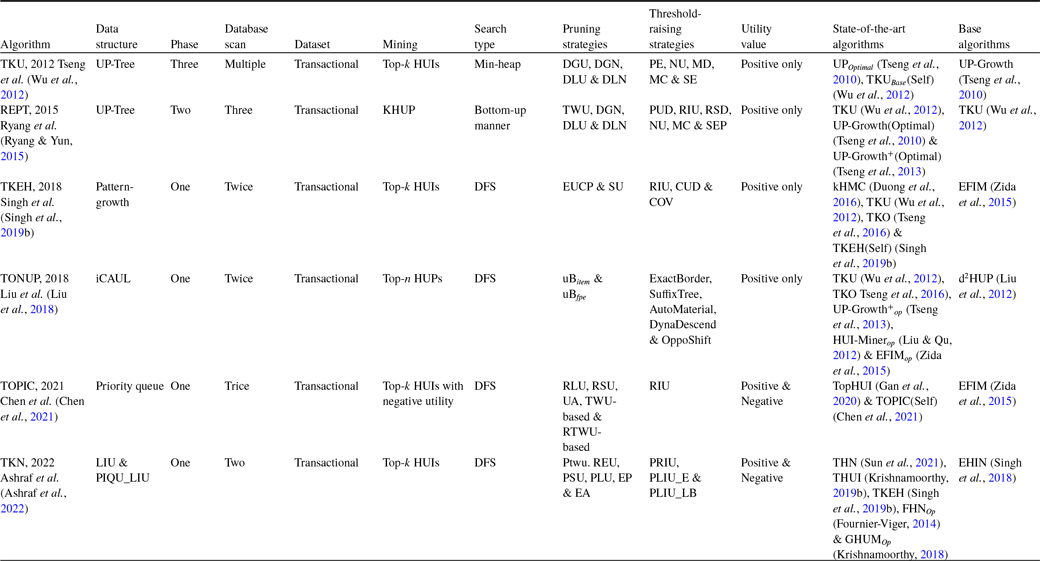
Table 9. Advantages and disadvantages of the tree-based top-k HUIM algorithms for the static datasets
3.1.2 Incremental and data stream based algorithms
Several HUIM algorithms are proposed from data stream datasets (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Choi2012). However, static dataset based algorithms cannot be applied in the case of data streams because of the following reasons: (1) data are coming rapidly, (2) unknown or unlimited data size, and (3) inability to know previous transactions. To address these challenges, the HUIM method for data stream (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Choi2012) is proposed to efficiently discover the HUIs. However, it takes lots of time to process the data from the data stream. Moreover, the user is required to set a minimum utility threshold. To resolve these issues, the top-k HUIM algorithm (Wu et al., Reference Wu, Shie, Tseng and Yu2012) is designed to mine top-k HUIs without specifying the minimum-utility threshold. However, this method works only for static data. Moreover, it requires high runtime and memory utilization. In this sub-section, we provide an up-to-date discussion about the incremental and data stream dataset-based top-k HUIM algorithms.
The conventional top-k HUIM algorithms (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Ryang & Yun, Reference Ryang and Yun2015; Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) are not suitable for the data stream because the number of items grows exponentially, thereby failing to identify top-k HUIs. To resolve this problem, Zihayat and An (Reference Zihayat and An2014) proposed the pattern-growth approach, named T-HUDS (Top-k High Utility itemset mining over Data Stream), the first work of its kind, to mine the top-k high utility patterns over a sliding window from the data stream. The authors proposed four strategies to automatically initialise and dynamically adjust the minimum-utility threshold. The first three strategies are performed during the first phase, while the fourth strategy is performed during the second phase of the mining process. The first strategy uses a novel estimation utility model, named prefix utility, to find HUIs and a closer estimation of true utility than TWU. The second strategy initialises the threshold using the Maximum Utility List (maxUtilList). It is computed during the construction and updating of the HUDS-tree. The third strategy adjusts the threshold using the Minimum Itemset Utility List (MIUList) by dynamically adjusting the threshold and storing the top-k Minimum Itemsets Utility (MIU) values of current promising HUIs. The fourth strategy adjusts the threshold with the minimum top-k utility (minTopKUtil) of the previous window. It uses a compressed tree structure, named High Utility Data Stream Tree (HUDS-tree), like FP-tree (Han et al., Reference Han, Pei and Yin2000), to keep the details about the transactions in the sliding window. HUDS-tree is built in one dataset scan only. In phase one, HUDS-tree is mined to generate the Potential top-k HUIs (PTKHUIs), while in phase two, the exact utility of PTKHUIs is calculated to discover the top-k HUIs. To measure the effectiveness of the proposed strategies, two versions of T-HUDS are developed, namely T-HUDS
![]() $_I$
and T-HUDS. The former utilises only the first three strategies during the first phase. On the other hand, T-HUDS uses all the strategies during the first and second phases of the mining process. To measure the effectiveness of threshold-raising strategies in phase one, three versions of the proposed algorithms, namely T-HUDS
$_I$
and T-HUDS. The former utilises only the first three strategies during the first phase. On the other hand, T-HUDS uses all the strategies during the first and second phases of the mining process. To measure the effectiveness of threshold-raising strategies in phase one, three versions of the proposed algorithms, namely T-HUDS
![]() $_1$
, T-HUDS
$_1$
, T-HUDS
![]() $_2$
, and T-HUDS
$_2$
, and T-HUDS
![]() $_3$
, are evaluated. It is observed that T-HUDS
$_3$
, are evaluated. It is observed that T-HUDS
![]() $_3$
performs better than both T-HUDS
$_3$
performs better than both T-HUDS
![]() $_1$
and T-HUDS
$_1$
and T-HUDS
![]() $_2$
, while T-HUDS
$_2$
, while T-HUDS
![]() $_2$
performs better than T-HUDS
$_2$
performs better than T-HUDS
![]() $_1$
. The comparison of these versions, T-HUDS
$_1$
. The comparison of these versions, T-HUDS
![]() $_1$
, T-HUDS
$_1$
, T-HUDS
![]() $_2$
, and T-HUDS
$_2$
, and T-HUDS
![]() $_3$
, is shown in Table 10.
$_3$
, is shown in Table 10.
Table 10. Comparison of three designed versions of the T-HUDS algorithm using different threshold-raising strategies (Zihayat & An, Reference Zihayat and An2014)

T-HUDS outperforms the state-of-the-art algorithm, HUPMS
![]() $_T$
(Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Choi2012) (Basic version of TKU Wu et al., Reference Wu, Shie, Tseng and Yu2012), concerning the number of obtained candidates, threshold, first and second phase time, total runtime, memory usage, window size, and scalability on dense and sparse datasets. However, the sliding window of the proposed algorithm cannot be entirely kept in memory, which may lead to more database scans. Moreover, the HUDS-tree is a lossy compression of the transactions in the sliding window, which may make it difficult to obtain the exact utility of the PTKHUIs.
$_T$
(Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Choi2012) (Basic version of TKU Wu et al., Reference Wu, Shie, Tseng and Yu2012), concerning the number of obtained candidates, threshold, first and second phase time, total runtime, memory usage, window size, and scalability on dense and sparse datasets. However, the sliding window of the proposed algorithm cannot be entirely kept in memory, which may lead to more database scans. Moreover, the HUDS-tree is a lossy compression of the transactions in the sliding window, which may make it difficult to obtain the exact utility of the PTKHUIs.
The main issues of the top-k HUIM approach from data streams, based on the concept of sliding window, follow as follows: (1) How do you maintain the window and keep the utility information of itemsets because the old data needs to be deleted as the new data arrives? (2) How do you discover the top-k HUIs for the sliding window? To solve these problems, Lu et al. (Reference Lu, Liu and Wang2014a) developed an effective sliding window-based method, named TOPK-SW (Top-k high utility itemset mining based on Sliding-Window), to mine the top-k HUIs without candidate generations from the data stream. It performs two main tasks: (1) maintains the data in the current window. (2) mines top-k high utility itemsets on the window. A novel tree structure, named High Utility Itemsets Tree (HUI-Tree), is proposed to maintain the information about the item’s utility in lexicographical order and store each batch of data in the current window. It does not require additional dataset scans. Experiments show that TOPK-SW outperforms the optimal case of the state-of-the-art UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) for the runtime and number of generated patterns from the dense and sparse datasets. TOPK-SW also significantly outperforms the UP(Optimal) in terms of time and space efficiency on dense and long transactional datasets. It is observed that the time efficiency of TOPK-SW can be significantly improved up to one order of magnitude in the case of dense and long transactional datasets. Moreover, the proposed algorithm is more stable as there are variations in the value of k.
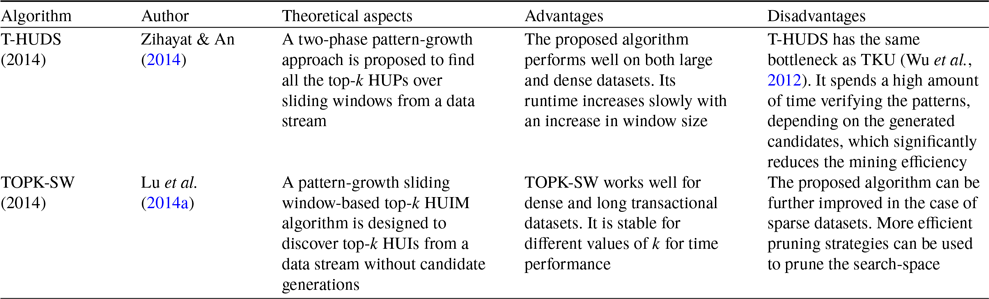
Table 11 describes the comparative overview of the tree-based top-k HUIM algorithms for increment and data stream datasets. Table 12 highlights the pros and cons of all the currently available tree-based top-k HUIM algorithms for increment and data stream datasets.
Table 11. An overview of the tree-based top-k HUIM algorithms for increment and data stream datasets

Table 12. Advantages and disadvantages of the tree-based top-k HUIM algorithms for increment and data stream datasets
3.1.3 Sequential dataset-based algorithms
Traditional HUIM algorithms (Liu et al., Reference Liu and Liao2005; Liu & Qu, Reference Liu and Qu2012) cannot be applied to the sequential datasets that consist of the itemsets with sequence related information. To address this issue, high-utility sequential pattern mining (HUSPM) algorithm (Yin et al., Reference Yin, Zheng and Cao2012) is proposed to find the high-utility sequential patterns (HUSPs) from the sequential datasets. However, they incur the following challenges: (1) It is hard to set the appropriate threshold because users are unaware of the characteristics of datasets. (2) It takes lots of time to extract the exact number of intended patterns. To address these issues, top-k HUSPM algorithms are proposed, inspired by top-k SPM (Tzvetkov et al., Reference Tzvetkov, Yan and Han2003) and top-k HUIM (Wu et al., Reference Wu, Shie, Tseng and Yu2012), to mine top-k HUSPs. However, there are the following challenges: (1) It is computationally infeasible to prune the search-space. (2) combinatorial explosion of search-space; (3) identification of all top-k HUSPs. In this sub-section, we provide an up-to-date discussion about the sequential dataset-based top-k HUIM algorithms.
The mining of top-k high utility sequential itemsets is an arduous task than that of top-k HUIs for several reasons: (1) The DCP does not hold for top-k high-utility sequences; hence, top-k frequent sequence pattern mining (Tzvetkov et al., Reference Tzvetkov, Yan and Han2003) cannot be straight-forwardly applicable to high-utility sequences. (2) Computational complexity and combinatorial explosion are very high because of the sequencing among itemsets. (3) Raising the minimum threshold is difficult without any loss of the top-k high utility sequential itemsets. To address these issues, Yin et al. (Reference Yin, Zheng, Cao, Song and Wei2013) proposed a method, named TUS (Top-k high Utility Sequence mining), to discover the top-k utility sequences without minimum-utility threshold from the sequential datasets. The authors developed a baseline method, named TUSNaive, to mine the top-k sequential itemsets with high utilities. It adopts the TUSList structure to keep the top-k HUSPs on-the-fly. However, TUSNaive traverses excessive invalid sequences as the minimum threshold begins with 0, thereby reducing the mining performance. To address this issue, three effective strategies are designed. Firstly, the pre-insertion strategy is designed to raise the minimum threshold to stop unwanted candidate generations. Secondly, the sorting concatenation order strategy is performed to effectively identify the promising high-utility sequences. Lastly, a sequence-reduced utilisation (SRU) strategy is applied to maintain the tighter sequence boundary that keeps refreshing the blacklist until all the items in the whitelist satisfy the minimum-utility threshold value.
Three versions of the baseline algorithm, TUSNaive, are designed, namely TUSNaive+ (TUSNaive with SRU), TUSNaive+I (TUSNaive with SRU and pre-insertion), and TUSNaive+S (TUSNaive with SRU and sorting). It is observed that TUS, TUSNaive+I, and TUSNaive+S perform better than TUSNaive+. TUSNaive+I performs better than TUSNaive+S for small values of k, while TUSNaive+S performs better than TUSNaive+I when k exceeds a certain number. Hence, the proposed optimisation measures–SRU, sorting, and pre-insertion–significantly extract the top-k patterns. The experiments are performed on two syntactic datasets and two real datasets, show that TUS performs 10 to 1000 times faster than the baseline algorithm, TUSNaive.
Rathore et al. (Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016) proposed an effective method, named TUP (Top-k Utility ePisode mining), to mine the top-k high-utility episode from a complex event sequence. The authors developed a basic method, named TUP-Basic, to dynamically keep the sorted list of size k that consists of the top-k HUEs. TUP-basic calculates the minimum occurrence, utility, and Episode-Weighted Utilization (EWU) of 1-length episodes by scanning the dataset only once. But it generates numerous candidates because the threshold starts at 0. It is highly computationally expensive to extract the number of items in the exponential search-space. To raise the minimum utility threshold, an effective Pre-insertion strategy is proposed to pre-insert the event sets concurrently. It raises the minimum utility threshold from 0 to 13 before the start of the mining process. To further enhance the efficiency of the mining process, the EWU strategy is proposed to effectively deal with frequency and utility. It explores those episodes first that have a high EWU value. The TUP-combined strategy combines the features of both the pre-insertion and EWU strategies. The effectiveness of pre-insertion, TUP-EWU, and TUP-Combined is measured for runtime and memory usage. It is observed that the pre-insertion strategy performs better for the total runtime and number of generated candidate episodes on the sparse datasets. On the other hand, TUP-EWU and TUP-Combined perform better for total runtime and memory usage on dense datasets. However, the performance of TUP-EWU is worse on sparse datasets because of a few short high-utility episodes.
Sequential pattern mining is widely used to extract gene regulation sequential patterns. However, it incurs the following challenges: (1) It depends on the frequency or support. (2) It is a tedious task to determine the threshold value. One possible solution is to design top-k HUP algorithms to efficiently work on gene regulation. But the major issues are: (1) The threshold is unknown in advance. (2) raise the threshold with the complete set of top-k patterns. To resolve these problems, Zihayat et al. (Reference Zihayat, Davoudi and An2016) proposed a novel algorithm, named TU-SEQ (Top-k Utility-based gene regulation SEQuential pattern discovery), the first work of its kind, that considers the utility model in terms of the gene importance and degree of expression to mine the top-k high utility gene regulation sequential patterns (top-k HUGSs). TU-SEQ only needs a user-specified number k and disease as an objective to traverse the k most high-utility gene regulation sequences that guarantee to give the complete set of top-k patterns. The authors proposed a baseline algorithm, named TU-SEQ
![]() $_{Base}$
, an extension of the threshold-based approach, HUSP-Stream (Zihayat et al., Reference Zihayat, Wu, An and Tseng2015) and adopt ItemUtilLists and HUSP-Tree, to keep the details of promising top-k HUGSs. ItemUtilLists is a vertical representation of the time samples in the dataset; on the other hand, HUSP-Tree is a lexicographic sequence tree that is constructed recursively in a top-down manner using ItemUtilLists, where each non-root node represents a sequence of gene-sets. TU-SEQ
$_{Base}$
, an extension of the threshold-based approach, HUSP-Stream (Zihayat et al., Reference Zihayat, Wu, An and Tseng2015) and adopt ItemUtilLists and HUSP-Tree, to keep the details of promising top-k HUGSs. ItemUtilLists is a vertical representation of the time samples in the dataset; on the other hand, HUSP-Tree is a lexicographic sequence tree that is constructed recursively in a top-down manner using ItemUtilLists, where each non-root node represents a sequence of gene-sets. TU-SEQ
![]() $_{Base}$
constructs a fixed-size sorted list, named top-k HUGS List (TKList), to maintain the information of top-k HUGSs and their utility values. However, TU-SEQ
$_{Base}$
constructs a fixed-size sorted list, named top-k HUGS List (TKList), to maintain the information of top-k HUGSs and their utility values. However, TU-SEQ
![]() $_{Base}$
works efficiently, but it generates numerous non-valid sequence candidates because the minimum utility begins with 0, thereby reducing the mining performance. To enhance the mining performance, an efficient strategy, named Pre-Evaluation using genes and Sequences (PES), is proposed to initialise the threshold and TKList by inserting the utility of genes and sequences before the HUSP-Tree construction.
$_{Base}$
works efficiently, but it generates numerous non-valid sequence candidates because the minimum utility begins with 0, thereby reducing the mining performance. To enhance the mining performance, an efficient strategy, named Pre-Evaluation using genes and Sequences (PES), is proposed to initialise the threshold and TKList by inserting the utility of genes and sequences before the HUSP-Tree construction.
TU-SEQ compares with CTGR-Span (Cheng et al., Reference Cheng, Liu, Tsai and Tseng2013), and results show that TU-SEQ extracts patterns whose popularity is considerably high and useful to identify the relation between promising genes and others. The experimental results show the effectiveness of TU-SEQ over TU-SEQ
![]() $_{Base}$
(self) and HUSP-Stream (Zihayat et al., Reference Zihayat, Wu, An and Tseng2015) in terms of execution time on the GSE6377 dataset (McDunn et al., Reference McDunn, Husain, Polpitiya, Burykin, Ruan, Li, Schierding, Lin, Dixon, Zhang, Coopersmith, Dunne, Colonna, Ghosh and Cobb2008). TU-SEQ is more than five times quicker than TU-SEQ
$_{Base}$
(self) and HUSP-Stream (Zihayat et al., Reference Zihayat, Wu, An and Tseng2015) in terms of execution time on the GSE6377 dataset (McDunn et al., Reference McDunn, Husain, Polpitiya, Burykin, Ruan, Li, Schierding, Lin, Dixon, Zhang, Coopersmith, Dunne, Colonna, Ghosh and Cobb2008). TU-SEQ is more than five times quicker than TU-SEQ
![]() $_{Base}$
because of the PES strategy. For the larger value of k, TU-SEQ
$_{Base}$
because of the PES strategy. For the larger value of k, TU-SEQ
![]() $_{Base}$
cannot be completed in a significant amount of time. However, HUSP-Stream consumes less memory than that of TU-SEQ and TU-SEQ
$_{Base}$
cannot be completed in a significant amount of time. However, HUSP-Stream consumes less memory than that of TU-SEQ and TU-SEQ
![]() $_{Base}$
. The reason is that HUSP-Stream utilises an optimal threshold to prune the search-space, thus resulting in significant memory usage.
$_{Base}$
. The reason is that HUSP-Stream utilises an optimal threshold to prune the search-space, thus resulting in significant memory usage.
Traditional HUSPM algorithm (Yin et al., Reference Yin, Zheng and Cao2012) generates numerous candidates and scan the dataset multiple times. To address these issues, Wang et al. (Reference Wang, Huang and Chen2016) proposed HUS-Span to extract the HUSPs by visiting the lexicographical tree using depth-first search. Two upper bounds, namely Prefix Extension Utility (PEU) and Reduced Sequence Utility (RSU), and two pruning strategies are proposed to reduce the generated candidates. An efficient data structure, called the utility chain, is designed to accelerate the computational tasks of PEU, RSU, and utility sequences. HUS-Span first scans the dataset to accumulate the Sequence Weighted Utility (SWU) of each 1-sequence and then builds the utility-chains of 1-sequences satisfying the minimum utility threshold. However, the major issue of HUS-Span is setting the proper threshold. To resolve this issue, an efficient work is introduced for top-k HUSPM (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013) which uses the min-heap structure. It sets the value of k to mine the top-k patterns from the sequential datasets. The main problem with this approach is to rapidly pervade the min-heap data structure with a high utility sequence to improve mining performance. To solve this problem, the authors proposed an algorithm TKHUS-Span: (Top-k High Utility Sequential pattern mining) that has three variants, namely TKHUS-Span
![]() $_{GDFS}$
, TKHUS-Span
$_{GDFS}$
, TKHUS-Span
![]() $_{BFS}$
, and TKHUS-Span
$_{BFS}$
, and TKHUS-Span
![]() $_{Hybrid}$
, which are used to prune the search-space using a lexicographical tree as in Yin et al. (Reference Yin, Zheng, Cao, Song and Wei2013). TKHUS-Span
$_{Hybrid}$
, which are used to prune the search-space using a lexicographical tree as in Yin et al. (Reference Yin, Zheng, Cao, Song and Wei2013). TKHUS-Span
![]() $_{GDFS}$
visits the tree by using the Guided Depth-First Search (GDFS) that always visits child nodes first with the highest PEU value to complete the mining process. To further improve the performance, TKHUS-Span
$_{GDFS}$
visits the tree by using the Guided Depth-First Search (GDFS) that always visits child nodes first with the highest PEU value to complete the mining process. To further improve the performance, TKHUS-Span
![]() $_{BFS}$
is developed to explore the search-space by using Best-First Search (BFS) and max-heap data structures that visit the nodes according to their PEU value. TKHUS-Span
$_{BFS}$
is developed to explore the search-space by using Best-First Search (BFS) and max-heap data structures that visit the nodes according to their PEU value. TKHUS-Span
![]() $_{BFS}$
effectively raises the minimum-utility threshold than that of TKHUS-Span
$_{BFS}$
effectively raises the minimum-utility threshold than that of TKHUS-Span
![]() $_{GDFS}$
and TUS (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013), however, it consumes lots of memory. To alleviate the limitations of TKHUS-Span
$_{GDFS}$
and TUS (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013), however, it consumes lots of memory. To alleviate the limitations of TKHUS-Span
![]() $_{GDFS}$
and TKHUS-Span
$_{GDFS}$
and TKHUS-Span
![]() $_{BFS}$
, a hybrid approach, named TKHUS-Span
$_{BFS}$
, a hybrid approach, named TKHUS-Span
![]() $_{Hybrid}$
, is proposed to balance mining efficiency and space usage by applying both BFS and DFS. It first uses BFS where memory is limited, and then shifts to DFS where memory is not a constraint.
$_{Hybrid}$
, is proposed to balance mining efficiency and space usage by applying both BFS and DFS. It first uses BFS where memory is limited, and then shifts to DFS where memory is not a constraint.
The experimental results prove the effectiveness of HUS-Span over the benchmark algorithm, USpan (Yin et al., Reference Yin, Zheng and Cao2012), in terms of a utility threshold effect, number of generated candidates, projected dataset scans, runtime, dataset size, and scalability from dense and sparse datasets. It is observed that TKHUS-Span
![]() $_{BFS}$
outperforms TKHUS-Span
$_{BFS}$
outperforms TKHUS-Span
![]() $_{GDFS}$
, TKHUS-Span
$_{GDFS}$
, TKHUS-Span
![]() $_{Hybrid}$
, and TUS under different values of k. TKHUS-Span
$_{Hybrid}$
, and TUS under different values of k. TKHUS-Span
![]() $_{BFS}$
and (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013)TKHUS-Span
$_{BFS}$
and (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013)TKHUS-Span
![]() $_{Hybrid}$
perform better than TKHUS-Span
$_{Hybrid}$
perform better than TKHUS-Span
![]() $_{GDFS}$
and TUS when k is large enough. TKHUS-Span
$_{GDFS}$
and TUS when k is large enough. TKHUS-Span
![]() $_{BFS}$
generates 180 times less number of candidates than that of TUS when k = 10 000. TKHUS-Span
$_{BFS}$
generates 180 times less number of candidates than that of TUS when k = 10 000. TKHUS-Span
![]() $_{BFS}$
is 45 times faster than TKHUS-Span
$_{BFS}$
is 45 times faster than TKHUS-Span
![]() $_{GDFS}$
when k = 50. The reason is that TKHUS-Span
$_{GDFS}$
when k = 50. The reason is that TKHUS-Span
![]() $_{BFS}$
discovers top-k HUSPs at an early stage. However, TKHUS-Span
$_{BFS}$
discovers top-k HUSPs at an early stage. However, TKHUS-Span
![]() $_{BFS}$
suffers from high memory consumption. TKHUS-Span
$_{BFS}$
suffers from high memory consumption. TKHUS-Span
![]() $_{Hybrid}$
is utilised to balance between runtime and memory consumption.
$_{Hybrid}$
is utilised to balance between runtime and memory consumption.
Negative Sequential Patterns (NSP) mining refers to frequent sequences with Non-occurring Behavior (NOB) and occurring behavior which includes positive and negative behaviors in behavior sequential analysis (Zaki, Reference Zaki2001). NSP consists of more useful information than PSP (Positive Sequential Patterns).However, it incurs the following challenges: (1) How to mine the intended numbers of NSPs? (2) How to select useful NSPs? (3) How to reduce the high-time computation? To resolve these problems, Dong et al. (Reference Dong, Qiu, Lü, Cao and Xu2019) proposed an optimisation approach called Topk-NSP
![]() $^+$
(top-k Negative Sequential Patterns Mining algorithm), the first of its kind, to find useful top-k NSPs from the top-k PSPs without specifying the minimum threshold. Topk-NSP only mines top-k NSPs; it does not consider the efficiency of the mining process. Therefore, the Topk-NSP
$^+$
(top-k Negative Sequential Patterns Mining algorithm), the first of its kind, to find useful top-k NSPs from the top-k PSPs without specifying the minimum threshold. Topk-NSP only mines top-k NSPs; it does not consider the efficiency of the mining process. Therefore, the Topk-NSP
![]() $^+$
algorithm is proposed that improves over Topk-NSP by using three optimisation strategies, namely Weighted Support, Interestingness Metric, and Pruning Strategy. Therefore, the Topk-NSP
$^+$
algorithm is proposed that improves over Topk-NSP by using three optimisation strategies, namely Weighted Support, Interestingness Metric, and Pruning Strategy. Therefore, the Topk-NSP
![]() $^+$
algorithm is proposed that improves over Topk-NSP by using three optimization strategies, namely Weighted Support, Interestingness Metric, and Pruning Strategy. The first optimization strategy uses two weights,
$^+$
algorithm is proposed that improves over Topk-NSP by using three optimization strategies, namely Weighted Support, Interestingness Metric, and Pruning Strategy. The first optimization strategy uses two weights,
![]() $ w_P $
and
$ w_P $
and
![]() $ w_N $
, to denote the user preference values for NSPs and PSPs, respectively. It also utilizes Weight Support (wsup). The second optimization strategy is used to improve wsup. It uses metric weight support, denoted by iwsup. It integrates the concepts of metric weighted support and interestingness to efficiently change the top-k useful NSPs. But it consumes a high amount of time to obtain all iwsup. To solve this issue, a third optimisation strategy is used that only calculates a part of iwsup and prunes the unpromising operations. It consists of the following steps: (1) First, it builds the seed set. (2) Second, it prunes the seed set. Topk-NSP
$ w_N $
, to denote the user preference values for NSPs and PSPs, respectively. It also utilizes Weight Support (wsup). The second optimization strategy is used to improve wsup. It uses metric weight support, denoted by iwsup. It integrates the concepts of metric weighted support and interestingness to efficiently change the top-k useful NSPs. But it consumes a high amount of time to obtain all iwsup. To solve this issue, a third optimisation strategy is used that only calculates a part of iwsup and prunes the unpromising operations. It consists of the following steps: (1) First, it builds the seed set. (2) Second, it prunes the seed set. Topk-NSP
![]() $^+$
generates NSCs (Negative Sequential Candidates) by utilising the NSCgeneration method. It mines top-k NSPs from top-k PSPs without scanning the dataset.
$^+$
generates NSCs (Negative Sequential Candidates) by utilising the NSCgeneration method. It mines top-k NSPs from top-k PSPs without scanning the dataset.
It is observed that Topk-NSP takes 0.01 percent to 3 percent less execution time than that of top-k PSP over the benchmark datasets. The reason is that Topk-NSP does not require re-scanning the dataset. The experimental results show the efficiency of the Topk-NSP
![]() $^+$
over Topk-NSP in terms of computational cost and scalability on the benchmark datasets. When there is a five-fold increase in data size, the memory consumption increases only about two times. Therefore, Topk-NSP
$^+$
over Topk-NSP in terms of computational cost and scalability on the benchmark datasets. When there is a five-fold increase in data size, the memory consumption increases only about two times. Therefore, Topk-NSP
![]() $^+$
effectively prunes the seed sets and unpromising operations, thereby significantly improving the time efficiency. However, there is a need to verify the correctness and completeness of the patterns discovered by the designed approach.
$^+$
effectively prunes the seed sets and unpromising operations, thereby significantly improving the time efficiency. However, there is a need to verify the correctness and completeness of the patterns discovered by the designed approach.
Although top-k HUSPM algorithms are simple, user-friendly, and straightforward in implementation, they incur the following challenges: (1) combinatorial explosion of search-space. (2) It is computationally impractical to prune the search-space. (3) identification of all top-k patterns. To address these issues, Zhang et al. (Reference Zhang, Du, Gan and Yu2021) designed a TKUS (Mining Top-K high Utility Sequential patterns) algorithm to discover the complete set of top-k HUSPs without specifying the minimum-utility threshold. TKUS utilises projection and local search mechanisms to scan the dataset only once. It builds the dataset recursively by constructing the projected datasets of current candidates and expanding it using the divide-and-conquer approach to greatly prune the search-space, especially when it calculates the utilities of long candidates. The LQS-Tree structure (Yin et al., Reference Yin, Zheng and Cao2012), an extension of the lexicographic sequence tree (Ayres et al., Reference Ayres, Flannick, Gehrke and Yiu2002), is used to represent the search tree. An utility-chain structure (Wang et al., Reference Wang, Huang and Chen2016) consists of utility lists and is used to minimise the computational cost. A threshold-raising strategy, called Sequence Utility Raising (SUR), is incorporated to raise the threshold in advance to an acceptable level to effectively prune the non-promising candidates early. Three utility upper bounds, namely sequence-weighted utilization (SWU), sequence-projected utilization (SPU), and sequence extension utility (SEU), are proposed to efficiently prune the search-space. Two tight upper bounds, namely PEU and RSU (Wang et al., Reference Wang, Huang and Chen2016), are also incorporated to further reduce the search-space, resulting in the acceleration of the mining process to a reasonable level. Two pruning strategies, namely Terminate Descendants Early (TDE) and Eliminate Unpromising Items (EUI), are proposed to greatly prune the search-space. TDE is a depth-based strategy that can stop the scanning of deep but non-promising nodes in the LQS-tree. On the other hand, EUI is a width-based strategy to prevent the proposed algorithm from scanning the new branches in the LQS-tree. Three variants of the proposed algorithm, namely TKUS
![]() $_{SUR}$
, TKUS
$_{SUR}$
, TKUS
![]() $_{TDE}$
, and TKUS
$_{TDE}$
, and TKUS
![]() $_{EUI}$
, are designed to measure the effectiveness of the pruning strategies. It has been observed that these variants perform well in most cases. The experimental results prove that TKUS outperforms the state-of-the-art algorithm TKHUS-Span (Wang et al., Reference Wang, Huang and Chen2016) in terms of execution time, memory usage, elimination of non-promising candidates, and scalability. A new metric, named search-space Shrinkage Rate (SSSR), is designed to compare the reduction of space of the proposed algorithm with the TKHUS-Span. The proposed algorithm generates fewer candidates than the benchmark algorithm. However, TKUS consumes more memory for some benchmark datasets because it needs high storage space to maintain the utility and PEU values of all 1-sequences and 2-sequences along with the SUR strategy.
$_{EUI}$
, are designed to measure the effectiveness of the pruning strategies. It has been observed that these variants perform well in most cases. The experimental results prove that TKUS outperforms the state-of-the-art algorithm TKHUS-Span (Wang et al., Reference Wang, Huang and Chen2016) in terms of execution time, memory usage, elimination of non-promising candidates, and scalability. A new metric, named search-space Shrinkage Rate (SSSR), is designed to compare the reduction of space of the proposed algorithm with the TKHUS-Span. The proposed algorithm generates fewer candidates than the benchmark algorithm. However, TKUS consumes more memory for some benchmark datasets because it needs high storage space to maintain the utility and PEU values of all 1-sequences and 2-sequences along with the SUR strategy.
Although the top-k utility episode mining (TUP) algorithm (Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016) performed significant work, there is still vast scope for further improvement. Wan et al. (Reference Wan, Chen, Gan, Chen and Goyal2021) proposed a faster and more efficient algorithm, named THUE (Discovering Top-k High Utility Episodes), based on the UMEpi algorithm (Gan et al., Reference Gan, Lin, Chao and Yu2023), to discover the complete set of HUIs within the complex event sequences. It uses a prefix-shared tree, named lexicographical sequence tree (LS-tree), that consists of all the candidate episode information to reduce the search-space using the depth-first method. However, the number of episodes is extremely high, resulting in infeasible solutions to the exhaustive search. A pruning strategy, Episode-Weighted Utilization (EWU) (Guo et al., Reference Guo, Zhang, Liu, Chen, Zhu, Guan, Luo, Yu and Li2014), is used as an upper bound on the utility of episodes to accelerate the mining speed. However, EWU is loosely upper-bound; hence, it cannot discover all high episodes (Guo et al., Reference Guo, Zhang, Liu, Chen, Zhu, Guan, Luo, Yu and Li2014), Therefore, to provide a tighter upper bound, two pruning strategies, namely episode-weighted downward closure (EWDC) and optimized EWU (EWU
![]() $_{opt}$
) (Gan et al., Reference Gan, Lin, Chao and Yu2023). are adopted to significantly reduce the search-space, thereby resulting in the enhancement of the mining process. Three threshold-raising strategies, RIU (Ryang & Yun, Reference Ryang and Yun2015), RTU (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020), and RUC (Wu et al., Reference Wu, Shie, Tseng and Yu2012), are adopted to effectively raise the threshold. Three versions of the proposed algorithm, namely THUE
$_{opt}$
) (Gan et al., Reference Gan, Lin, Chao and Yu2023). are adopted to significantly reduce the search-space, thereby resulting in the enhancement of the mining process. Three threshold-raising strategies, RIU (Ryang & Yun, Reference Ryang and Yun2015), RTU (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020), and RUC (Wu et al., Reference Wu, Shie, Tseng and Yu2012), are adopted to effectively raise the threshold. Three versions of the proposed algorithm, namely THUE
![]() $_{ewu}$
, THUE
$_{ewu}$
, THUE
![]() $_{rus}$
, and THUE, are designed to evaluate the effectiveness of the adopted strategies. THUE
$_{rus}$
, and THUE, are designed to evaluate the effectiveness of the adopted strategies. THUE
![]() $_{ewu}$
uses RTU and RUC but excludes the RIU strategy. THUE
$_{ewu}$
uses RTU and RUC but excludes the RIU strategy. THUE
![]() $_{rus}$
uses the RIU strategy but does not include the EWU pruning strategy. THUI uses all strategies. It is observed that THUI outperforms THUE
$_{rus}$
uses the RIU strategy but does not include the EWU pruning strategy. THUI uses all strategies. It is observed that THUI outperforms THUE
![]() $_{ewu}$
and THUE
$_{ewu}$
and THUE
![]() $_{rus}$
in all cases. THUE performs better than the existing algorithm, TUP (Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016) for execution time, memory consumption, and scalability.
$_{rus}$
in all cases. THUE performs better than the existing algorithm, TUP (Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016) for execution time, memory consumption, and scalability.
Table 13 describes the overview of the strategies used in tree-based top-k HUSPM algorithms for the sequential datasets. Table 14 highlights the pros and cons of the tree-based top-k HUSPM algorithms for the sequential datasets.
Table 13. An overview of the tree-based top-k HUSPM algorithms for the sequential datasets
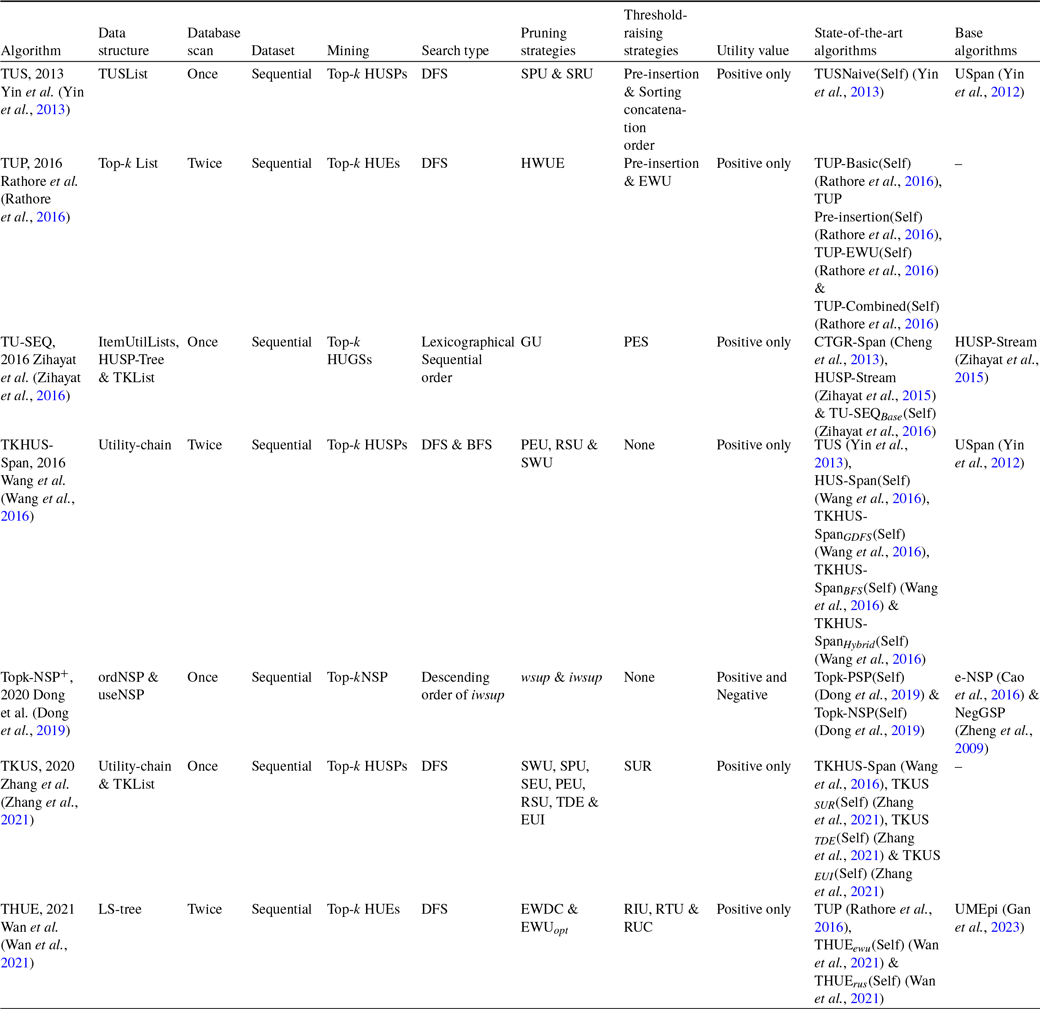
Table 14. Advantages and disadvantages of the tree-based top-k HUSPM algorithms for the sequential datasets

3.2 Utility-list-based top-k HUIM algorithms
The utility-list-based top-k HUIM algorithms are categorised into two parts: basic utility-list and extended utility-list based algorithms.
3.2.1 Basic utility-list-based algorithms
As we have seen previously, tree-based top-k HUIM algorithms (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Ryang & Yun, Reference Ryang and Yun2015) follow the general process to raise the minimum utility threshold from 0. The efficiency of the algorithm depends not only on the data structures and pruning strategies but also on how to quickly raise the threshold value to prune the search-space effectively. When the algorithm terminates, they should not miss any top-k HUIs in the mining process. Two-phase top-k HUIM algorithms (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Ryang & Yun, Reference Ryang and Yun2015; Zihayat & An, Reference Zihayat and An2014) scan the dataset multiple times and generate numerous unpromising candidates. They even do not work in the case of a large dataset with long transactions and large itemsets. To solve these issues, one-phase top-K HUIM methods (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016; Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) are developed to mine top-k HUIs from the large datasets. In this sub-section, we provide an up-to-date analysis of the basic utility-list-based top-k HUIM algorithms.
Tseng et al. developed two effective methods, namely TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) and TKO (Mining Top-k utility itemsets in One-phase) (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), to mine the top-k HUIs without the need to set the minimum-utility threshold from the transactional datasets. TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) is the two-phase tree-based algorithm, already discussed in detail in Section 3 and Table 8. TKO is a one-phase utility-list-based algorithm that adopts the utility structure of HUI-Miner (Liu & Qu, Reference Liu and Qu2012) and computes the utility of itemsets without the requirement of an original dataset scan. The authors proposed a basic version of TKO, called TKO
![]() $_{Base}$
, using the min-heap structure to raise the border threshold. It uses a strategy named Raising the threshold by the Utilities of Candidates (RUC), which incorporates the TopK-CI-List data structure, to mine top-k HUIs. TKO adopts two strategies, namely, Pre-Evaluation (PE) (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and Discarding Global Unpromising items (DGU) (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), while two strategies are proposed, namely, Reducing estimated Utility values by using Z-elements (RUZ) and Exploring the most Promising Branches first (EPB), to effectively reduce the search-space. RUZ is performed during the candidates’ generation process to search the top-k HUIs, while EPB generates the candidates with high utility first. Because the proposed algorithm raises the minimum border utility threshold at an early stage, it rapidly reduces the search-space. The experimental results show the effectiveness of TKO against TKU(Self) (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), REPT (Ryang & Yun, Reference Ryang and Yun2015) and the optimal case of the state-of-the-art, UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) and HUI-Miner (Liu & Qu, Reference Liu and Qu2012), concerning the runtime, memory usage, and scalability on dense and sparse datasets.
$_{Base}$
, using the min-heap structure to raise the border threshold. It uses a strategy named Raising the threshold by the Utilities of Candidates (RUC), which incorporates the TopK-CI-List data structure, to mine top-k HUIs. TKO adopts two strategies, namely, Pre-Evaluation (PE) (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and Discarding Global Unpromising items (DGU) (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), while two strategies are proposed, namely, Reducing estimated Utility values by using Z-elements (RUZ) and Exploring the most Promising Branches first (EPB), to effectively reduce the search-space. RUZ is performed during the candidates’ generation process to search the top-k HUIs, while EPB generates the candidates with high utility first. Because the proposed algorithm raises the minimum border utility threshold at an early stage, it rapidly reduces the search-space. The experimental results show the effectiveness of TKO against TKU(Self) (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), REPT (Ryang & Yun, Reference Ryang and Yun2015) and the optimal case of the state-of-the-art, UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) and HUI-Miner (Liu & Qu, Reference Liu and Qu2012), concerning the runtime, memory usage, and scalability on dense and sparse datasets.
Duong et al. (Reference Duong, Liao, Fournier-Viger and Dam2016) proposed an efficient approach, called kHMC (Top-k High utility itemset Mining using Co-occurrence pruning), to mine the top-k HUIs using depth-first search from the transactional datasets. Two effective pruning strategies, namely the Estimated Utility Co-occurrence Pruning Strategy with Threshold (EUCPT) and the Transitive Extension Pruning strategy (TEP), are proposed to reduce the search-space. The first strategy, EUCPT, adopts an efficient data structure, named Estimated Utility Co-occurrence Structure with Threshold (EUCST), to eliminate the excessive number of join operations. EUCPT is the refinement of the Estimated Utility Co-occurrence Pruning (EUCP) strategy as used in Fournier-Viger et al. (Reference Fournier-Viger, Wu, Zida and Tseng2014). The EUCST is constructed during the second dataset scan and requires a small amount of memory and rapid updates to mine the top-k HUIs. EUCPT reduces up to 95 percent of candidates as compared to FHM (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014). The second strategy, TEP, prunes the search-space by adopting a novel upper bound on the utilities of itemsets and their extensions. It creates the single items during the initial dataset scan and applies them after the EUCPT strategy. It significantly reduces the number of extensions to mine HUIs using utility lists and reduces up to 21 percent more candidates. kHMC presents a new utility-list construction method using utility-list (Liu & Qu, Reference Liu and Qu2012) to find HUIs in a single phase only. It keeps details regarding the utilities of itemsets and rapidly computes the utilities by combining the utility lists of smaller itemsets. It utilises the early abandoning (EA) strategy to terminate the utility-list construction at an early stage if it leads to the non-result of the top-k HUIs. It significantly minimises execution time and memory usage. Three threshold strategies, namely Real Item Utilities (RIU), raising the threshold based on Co-occurrence with Utility Descending order (CUD), and raising the threshold based on COVerage with utility descending order (COV), are used to initialise and dynamically adjust the border threshold. RIU is performed during the first scan, while CUD and COV are performed during the second scan. RIU calculates the utilities of all itemsets during the first scan and effectively raises the minimum utility threshold. CUD increases the minimum-utility threshold using the utilities of 2-itemsets stored in the EUCST. RSD and PUD strategies used by REPT (Ryang & Yun, Reference Ryang and Yun2015) are special cases of CUD strategies. CUD incorporates all the cases of RSD and PUD, thus showing a higher performance of almost 100 percent as compared to these strategies, and is also reasonable to be executed for runtime and memory usage. REPT scans the dataset three times, while kHMC scans only twice. COV adopts a COVerage List (COVL) structure that consists of a list of utility values. These strategies are very effective in raising the border threshold, which is very close to the true utility of itemsets. These strategies also ensure that no top-k HUIs are missed during the mining process. The notion of coverage is employed in HUIM algorithms to reduce the search-space. It is used by the proposed algorithm to raise the minimum utility threshold without additional dataset scans.
The authors proposed two versions of kHMC, namely kHMC
![]() $_{Tep}$
and kHMC
$_{Tep}$
and kHMC
![]() $_{NoTep}$
, to show the effectiveness of the TEP strategy, and results show that kHMC
$_{NoTep}$
, to show the effectiveness of the TEP strategy, and results show that kHMC
![]() $_{NoTep}$
generates 21 percent fewer candidates than that of kHMC
$_{NoTep}$
generates 21 percent fewer candidates than that of kHMC
![]() $_{Tep}$
. It is observed that kHMC outperforms the state-of-the-art algorithms TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), REPT (Ryang & Yun, Reference Ryang and Yun2015), and TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) for the number of promising candidates, runtime, memory consumption, and scalability on dense, sparse, and large datasets. Furthermore, the execution time and memory usage of the proposed algorithm kHMC are significantly less than those of REPT (Ryang & Yun, Reference Ryang and Yun2015) when k is set to large values (
$_{Tep}$
. It is observed that kHMC outperforms the state-of-the-art algorithms TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), REPT (Ryang & Yun, Reference Ryang and Yun2015), and TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) for the number of promising candidates, runtime, memory consumption, and scalability on dense, sparse, and large datasets. Furthermore, the execution time and memory usage of the proposed algorithm kHMC are significantly less than those of REPT (Ryang & Yun, Reference Ryang and Yun2015) when k is set to large values (
![]() $ 50 \le k \le 1000 $
). The reason is that REPT consumes a significant amount of time to enumerate 2-itemsets consisting of promising itemsets for each transaction. However, more effective pruning and threshold-raising strategies could be designed for further improve the mining process of the proposed algorithm.
$ 50 \le k \le 1000 $
). The reason is that REPT consumes a significant amount of time to enumerate 2-itemsets consisting of promising itemsets for each transaction. However, more effective pruning and threshold-raising strategies could be designed for further improve the mining process of the proposed algorithm.
The uncertain minimum utility of traditional top-k HUIM algorithms leads to more candidate generations and high memory usage. Lee and Park (Reference Lee and Park2016) proposed a new method, named TKUL-Miner (Top-k high utility itemset mining based on utility-list structures), to efficiently find the top-k HUIs. A utility-list is proposed to keep relevant details at each node of the search tree to mine the itemsets. The proposed algorithm scans the dataset twice and builds the data structures using min-heap, as in Fournier-Viger et al. (Reference Fournier-Viger, Wu, Zida and Tseng2014). Firstly, it scans the dataset to compute the TWU of each 1-itemset and rearranges it in ascending order of TWU. Secondly, it again scans the dataset to construct the utility list and EUCS structure. Two main algorithms of TKUL-Miner, namely, TKUL-FirstLevelSearch and TKUL-Search, are proposed. The first algorithm, TKUL-FirstLevelSearch, uses two strategies, namely First-level Search in TWU Decreasing-order (FSD) and Reducing the overestimated Utility by Sum
![]() $\_$
zrutils (RUZ). FSD searches 1-itemsets of the first level in the descending order of TWU, while RUZ effectively reduces the overestimated utilities of the itemsets. The second algorithm, TKUL-Search, further enhances the efficiency of pruning the search-space because it searches the itemsets in the ascending order of TWU and uses an efficient strategy named First child pruning by using Sum
$\_$
zrutils (RUZ). FSD searches 1-itemsets of the first level in the descending order of TWU, while RUZ effectively reduces the overestimated utilities of the itemsets. The second algorithm, TKUL-Search, further enhances the efficiency of pruning the search-space because it searches the itemsets in the ascending order of TWU and uses an efficient strategy named First child pruning by using Sum
![]() $\_$
Cutil (FCU). FCU significantly overestimates the utility of itemsets. These strategies, FSD, RUZ, and FCU, effectively raise the border threshold quickly and significantly prune the search-space. TKUL-FirstLevelSearch searches 1-itemsets and generates 2-itemsets; on the other hand, TKUL-Search searches and generates all the itemsets. The following notations are used to represent the different strategies of the proposed algorithm: (1) TKUL-base denotes TKUL-Miner without any strategy. (2) FLS denotes TKUL-base with FLS strategy. (3) RUZ denotes FLS and RUZ strategy. (4) TKUL-full denotes the full version of TKUL-Miner, including the FSD strategy. It is observed that TKUL-base performs worse execution time, while FLS is 70 percent faster than TKUL-base. RUZ also performs better than TKUL-base, but not very significantly as compared to FLS. Finally, TKUL-full shows almost a 20 percent improvement over TKUL-base. Overall, FLS performs better because it increases the minimum utility as quickly as mining the top-k HUIs. The experimental results prove the effectiveness and efficiency of the TKUL-Miner over benchmark algorithms TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), REPT (Ryang & Yun, Reference Ryang and Yun2015), and the optimal case of UP-Growth
$\_$
Cutil (FCU). FCU significantly overestimates the utility of itemsets. These strategies, FSD, RUZ, and FCU, effectively raise the border threshold quickly and significantly prune the search-space. TKUL-FirstLevelSearch searches 1-itemsets and generates 2-itemsets; on the other hand, TKUL-Search searches and generates all the itemsets. The following notations are used to represent the different strategies of the proposed algorithm: (1) TKUL-base denotes TKUL-Miner without any strategy. (2) FLS denotes TKUL-base with FLS strategy. (3) RUZ denotes FLS and RUZ strategy. (4) TKUL-full denotes the full version of TKUL-Miner, including the FSD strategy. It is observed that TKUL-base performs worse execution time, while FLS is 70 percent faster than TKUL-base. RUZ also performs better than TKUL-base, but not very significantly as compared to FLS. Finally, TKUL-full shows almost a 20 percent improvement over TKUL-base. Overall, FLS performs better because it increases the minimum utility as quickly as mining the top-k HUIs. The experimental results prove the effectiveness and efficiency of the TKUL-Miner over benchmark algorithms TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), REPT (Ryang & Yun, Reference Ryang and Yun2015), and the optimal case of UP-Growth
![]() $^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013) concerning the runtime and memory usage on dense, sparse, and long datasets. TKUL-Miner performs 10 times faster than REPT (Ryang & Yun, Reference Ryang and Yun2015) when k = 5000. The proposed algorithm also works better than other algorithms for varied values of k. TKUL-Miner is much faster, especially for dense and longer average-length datasets.
$^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013) concerning the runtime and memory usage on dense, sparse, and long datasets. TKUL-Miner performs 10 times faster than REPT (Ryang & Yun, Reference Ryang and Yun2015) when k = 5000. The proposed algorithm also works better than other algorithms for varied values of k. TKUL-Miner is much faster, especially for dense and longer average-length datasets.
Dam et al. (Reference Dam, Li, Fournier-Viger and Duong2017) proposed an effective utility-based method, called KOSHU (Top-k On-Shelf High Utility itemset miner with or without negative unit profits), the first of its kind, to mine all top-k high on-shelf utility itemsets by taking into consideration the on-shelf time periods of items with positive and/or negative profit values. KOSHU uses three effective strategies, namely Estimated co-occurrence Maximum Period Rate Pruning (EMPRP), Concurrence Existing of a pair 2-itemset Pruning (CE2P), and Period Utility Pruning (PUP), to prune the search-space and reduce the costly join operations. The first strategy, EMPRP, is based on a novel Estimated co-occurrence Maximum Period Rate Structure (EMPRS). KOSHU scans the dataset twice. In the first scan, it calculates the RTWU and utility of each item according to the increasing order of RTWU in such a way that all negative items succeed positive items. During the second scan, the EMPRS structure is constructed using a triangular matrix. However, a few pairs of items do not appear together in any transaction. Therefore, the second strategy for CE2P is to adopt the bit matrix to keep the information about 2-itemsets together. This strategy effectively works for sparse and large datasets. The third strategy, PUP, is to further reduce the search-space and costly join operations to enhance the mining process. The designed method also adopts two effective strategies, namely the Real 1-Itemset Relative Utilities threshold raising strategy (RIRU) and the Real 2-Itemset Relative Utilities threshold raising strategy (RIRU2), to initialise and dynamically adjust the internal relative utility threshold to enhance the mining performance. RIRU is inspired by the RIU strategy as described in Ryang and Yun (Reference Ryang and Yun2015) and is performed after the first scan. It calculates the relative utilities of all 1-itemsets, while RIRU2 is applied after the second scan to calculate the relative utility of all 2-itemsets. The EMPRS structure is constructed after RIRU and RIRU2 because it is built once and is used during the entire mining process. KOSHU includes a novel low-complexity optimisation procedure and a faster binary search method to construct the utility lists, as used in Liu and Qu (Reference Liu and Qu2012), Fournier-Viger et al. (Reference Fournier-Viger, Wu, Zida and Tseng2014), Tseng et al. (Reference Tseng, Wu, Fournier-Viger and Yu2016). It remembers the last search position index to start the next search from this position, resulting in a high-performance gain. The proposed algorithm adopts the Exploring the most Promising Branches first (EPB) strategy as used in Tseng et al. (Reference Tseng, Wu, Fournier-Viger and Yu2016) to extend the itemsets that have the largest estimated utility value first. Hence, it quickly raises the minimum utility threshold to reduce the search-space.
Experiments show that KOSHU performs better than the optimal cases of state-of-the-art, TS-HOUN (Lan et al., Reference Lan, Hong, Huang and Tseng2014) and FOSHU (Fournier-Viger & Zida, Reference Fournier-Viger and Zida2015) for runtime, memory utilisation, and scalability on the benchmark datasets. On the BMS-POS dataset, KOSHU outperforms the optimal case of FOSHU when
![]() $k \le 400$
, while it is slightly less than the optimal case of FOSHU for large values of k. On the other side, TS-HOUN (Lan et al., Reference Lan, Hong, Huang and Tseng2014) fails to terminate when
$k \le 400$
, while it is slightly less than the optimal case of FOSHU for large values of k. On the other side, TS-HOUN (Lan et al., Reference Lan, Hong, Huang and Tseng2014) fails to terminate when
![]() $k \ge 400$
. EMPRP and PUP, respectively, prune up to 89 percent and 93 percent of candidates. Therefore, PUP is more effective than EMPRP. Moreover, the utility list reduces execution time by up to 41 percent. It achieves high scalability in terms of the number of time periods because it mines all time periods concurrently. It also has high scalability in terms of the number of items and transactions. However, it is a little slow when the dataset consists of more time periods. Since KOSHU is the first algorithm to mine the top-k on-shelf HUIs. There is a wide scope for further improvement to build the approximate list of top-k high on-shelf utility itemsets mining.
$k \ge 400$
. EMPRP and PUP, respectively, prune up to 89 percent and 93 percent of candidates. Therefore, PUP is more effective than EMPRP. Moreover, the utility list reduces execution time by up to 41 percent. It achieves high scalability in terms of the number of time periods because it mines all time periods concurrently. It also has high scalability in terms of the number of items and transactions. However, it is a little slow when the dataset consists of more time periods. Since KOSHU is the first algorithm to mine the top-k on-shelf HUIs. There is a wide scope for further improvement to build the approximate list of top-k high on-shelf utility itemsets mining.
Le et al. (Reference Le, Truong and Tran2017) develop a non-candidate approach, named REPTPLUS (Enhancing Threshold-Raising Strategies for Effective Mining Top-k High Utility Patterns), to mine the top-k high utility patterns (HUPs) from the transactional dataset. REPTPLUS scans the dataset twice. In the first scan, it computes the actual utilities of items and saves the k highest utility items in the top-k HUIs list according to the ascending order of the utility. During the second scan, it constructs the initial utility list of items to raise the minimum utility threshold by using the RSD strategy. Then, it builds the utility list of k-itemsets (
![]() $k \ge 2$
) to find HUIs. It reuses the RIU strategy as used in Ryang and Yun (Reference Ryang and Yun2015) during the first scan. After that, it incorporates the RSD strategy to again raise the threshold during the second scan. It joins the utility lists of smaller itemsets (
$k \ge 2$
) to find HUIs. It reuses the RIU strategy as used in Ryang and Yun (Reference Ryang and Yun2015) during the first scan. After that, it incorporates the RSD strategy to again raise the threshold during the second scan. It joins the utility lists of smaller itemsets (
![]() $k \ge 2$
) to construct the utility list of k-itemsets (
$k \ge 2$
) to construct the utility list of k-itemsets (
![]() $k \ge 3$
). REPTPLUS adopts the utility-list structure according to the ascending order of TWU without generating the candidates. It does not use the given threshold to exploit the set of HUIs as used in UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), UP-Growth
$k \ge 3$
). REPTPLUS adopts the utility-list structure according to the ascending order of TWU without generating the candidates. It does not use the given threshold to exploit the set of HUIs as used in UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), UP-Growth
![]() $^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013), and MU-Growth (Yun et al., Reference Yun, Ryang and Ryu2014). REPTPLUS adopts the utility-list structure as per the increasing order of TWU, while REPT uses the UP-Tree structure as per the decreasing order of TWU. It uses two strategies, RIU and RSD, to raise the threshold in two scans, while REPT uses the two strategies, PUD and RIU, in the first scan. In the second scan, it builds the tree and further raises the threshold by using RSD and NU strategies. REPTPLUS uses a novel strategy for top-k real HUPs, while REPT uses the SEP strategy to process the top-k HUPs.
$^+$
(Tseng et al., Reference Tseng, Shie, Wu and Yu2013), and MU-Growth (Yun et al., Reference Yun, Ryang and Ryu2014). REPTPLUS adopts the utility-list structure as per the increasing order of TWU, while REPT uses the UP-Tree structure as per the decreasing order of TWU. It uses two strategies, RIU and RSD, to raise the threshold in two scans, while REPT uses the two strategies, PUD and RIU, in the first scan. In the second scan, it builds the tree and further raises the threshold by using RSD and NU strategies. REPTPLUS uses a novel strategy for top-k real HUPs, while REPT uses the SEP strategy to process the top-k HUPs.
It is observed that REPTPLUS outperforms the benchmark algorithm, REPT (Ryang & Yun, Reference Ryang and Yun2015) and the optimal case of the state-of-the-art algorithms, TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010) concerning the runtime and memory usage from the dense and synthetic datasets. REPTPLUS takes less time than REPT for
![]() $k \ge 20$
, while it consumes more time than REPT when
$k \ge 20$
, while it consumes more time than REPT when
![]() $k \lt 20$
. REPTPLUS significantly performs better for the large average length of the transactions in the dataset. However, there is a wide scope for improvement in the proposed algorithm for large and distributed datasets.
$k \lt 20$
. REPTPLUS significantly performs better for the large average length of the transactions in the dataset. However, there is a wide scope for improvement in the proposed algorithm for large and distributed datasets.
In the business scenario, the managers keep watch on the regular behaviour of customers and changes in customer behavior. A regular HUI denotes an itemset that appears at regular intervals specified by the customer in the transactional dataset. Two constraints, namely Minimum Utility (
![]() $min\_util$
) and Maximum Regularity (maxper), are defined to satisfy the itemsets.
$min\_util$
) and Maximum Regularity (maxper), are defined to satisfy the itemsets.
![]() $min\_util$
finds the minimum utility of an itemset, while maxper finds the maximum time difference between two consecutive itemsets in the dataset. Kumari et al. (Reference Kumari, Sanjeevi and Rao2019) proposed an efficient algorithm, named TKRHU miner (Top-k Regular High Utility Itemset miner), to mine all top-k RHUIs that appear regularly and specify
$min\_util$
finds the minimum utility of an itemset, while maxper finds the maximum time difference between two consecutive itemsets in the dataset. Kumari et al. (Reference Kumari, Sanjeevi and Rao2019) proposed an efficient algorithm, named TKRHU miner (Top-k Regular High Utility Itemset miner), to mine all top-k RHUIs that appear regularly and specify
![]() $min\_util$
, maxper, and minimum support, where k denotes the intended number of regular high itemsets. A novel list structure, named Regular Utility-lists (RUL), is designed to keep the information in each itemset compact format. The proposed algorithm scans the dataset twice: (1) During the first phase, the RULs of the 1-itemset are constructed to maintain both utility and regularity information. All itemsets are arranged according to their TWU value. Then, the Regular HUI miner algorithm is applied to find the complete set of RHUIs. It recursively mines top-k RHUIs by constructing the RULs of itemsets with length greater than 1. (2) During the second phase, the support of each RHUI is computed based on counting the number of elements that appear in each utility list. The TKRHU miner suffers from two bottlenecks: (1) During the initial stage, the unpromising candidate itemsets are pruned based on their TWUs. It does not take into consideration the regularity of itemsets that may lead to more memory consumption, search, and update of the RULs. (2) The number of RULs is quite large in the case of large datasets, which may lead to a computationally expensive procedure to obtain a comprehensive search of each utility list. To address these issues, the proposed algorithm TKRHU adopts the pruning strategy, named Early Abandoning (EA), that terminates the RULs construction process of unpromising itemsets by using the local periodicity upper bound. It is based on a greedy approach that significantly reduces the computational cost of the mining process.
$min\_util$
, maxper, and minimum support, where k denotes the intended number of regular high itemsets. A novel list structure, named Regular Utility-lists (RUL), is designed to keep the information in each itemset compact format. The proposed algorithm scans the dataset twice: (1) During the first phase, the RULs of the 1-itemset are constructed to maintain both utility and regularity information. All itemsets are arranged according to their TWU value. Then, the Regular HUI miner algorithm is applied to find the complete set of RHUIs. It recursively mines top-k RHUIs by constructing the RULs of itemsets with length greater than 1. (2) During the second phase, the support of each RHUI is computed based on counting the number of elements that appear in each utility list. The TKRHU miner suffers from two bottlenecks: (1) During the initial stage, the unpromising candidate itemsets are pruned based on their TWUs. It does not take into consideration the regularity of itemsets that may lead to more memory consumption, search, and update of the RULs. (2) The number of RULs is quite large in the case of large datasets, which may lead to a computationally expensive procedure to obtain a comprehensive search of each utility list. To address these issues, the proposed algorithm TKRHU adopts the pruning strategy, named Early Abandoning (EA), that terminates the RULs construction process of unpromising itemsets by using the local periodicity upper bound. It is based on a greedy approach that significantly reduces the computational cost of the mining process.
The experimental results show that the proposed algorithm TKRHU performs better than the optimal case of the state-of-the-art PHM (Fournier-Viger et al., Reference Fournier-Viger, Lin, Duong and Dam2016
b), in terms of execution time, number of determined nodes, memory usage, and scalability. It is observed that TKRHU is 200 times better than PHM (optimal) for
![]() $ (5 \le k \le 25) $
. The reason is that the proposed algorithm significantly reduces the number of comparisons of regular itemsets, resulting in a smaller number of candidate generations. However, for sparse datasets, for different values of k
$ (5 \le k \le 25) $
. The reason is that the proposed algorithm significantly reduces the number of comparisons of regular itemsets, resulting in a smaller number of candidate generations. However, for sparse datasets, for different values of k
![]() $ (5 \le k \le 30) $
, the execution time of the proposed algorithm TKRHU is moderately increased.
$ (5 \le k \le 30) $
, the execution time of the proposed algorithm TKRHU is moderately increased.
HUIM algorithms are extended to perform the task of High Utility Quantitative Itemset Mining (HUQIM) (Nouioua et al., Reference Nouioua, Fournier-Viger, Wu, Lin and Gan2021) to find the High Utility Quantitative Itemsets (HUQIs) that consist of cost-effective and quantity information. HUQIs give more information compared to HUIs; however, it is a quite challenging task to mine HUQIs. The reason is that different items and different quantities are considered to obtain the HUQIs. To solve this problem, Nouioua et al. (Reference Nouioua, Fournier-Viger, Gan, Wu, Lin, Nouioua, Li, Yue, Jiang, Chen, Li, Long, Fang and Yu2022) redefined the problem as top-k HUQIM and proposed an efficient algorithm, named TKQ (Top-K Quantitative itemset miner), that lets users directly obtain the k number of patterns without specifying the
![]() $min\_util$
threshold. The proposed algorithm is based on the utility-list structure that rapidly computes the utility of its associated Q-itemsets without performing the dataset scan. Three pruning strategies, namely TWU, Remaining utility, and Co-occurrence, are adopted to efficiently mine HUQIs. The TWU pruning strategy is an upper bound on the utility of Q-itemsets and their super-sets that is used to prune the unpromising Q-itemsets. The Remaining utility pruning strategy is based on the remaining utility (SumRutil) of Q-itemsets stored in their utility lists. The Co-occurrence pruning strategy is based on the TWU of Q-items Co-occurrence based Structure (TQCS) that is built during the second scan and finds all pairs of Q-itemsets along with their utility information. This strategy removes the Low Utility Quantitative Itemsets (LUQIs) with their transitive extensions without even building the utility lists. Two pruning strategies, namely the Exact Q-items Co-occurrence Pruning Strategy (EQCPS) and the Range Q-items Co-occurrence Pruning Strategy (RQCPS), are further adopted and are based on the TQCS structure. EQCPS and RQCPS are used to reduce unpromising exact and unpromising range Q-itemsets respectively. Three effective threshold strategies are adopted to raise the
$min\_util$
threshold. The proposed algorithm is based on the utility-list structure that rapidly computes the utility of its associated Q-itemsets without performing the dataset scan. Three pruning strategies, namely TWU, Remaining utility, and Co-occurrence, are adopted to efficiently mine HUQIs. The TWU pruning strategy is an upper bound on the utility of Q-itemsets and their super-sets that is used to prune the unpromising Q-itemsets. The Remaining utility pruning strategy is based on the remaining utility (SumRutil) of Q-itemsets stored in their utility lists. The Co-occurrence pruning strategy is based on the TWU of Q-items Co-occurrence based Structure (TQCS) that is built during the second scan and finds all pairs of Q-itemsets along with their utility information. This strategy removes the Low Utility Quantitative Itemsets (LUQIs) with their transitive extensions without even building the utility lists. Two pruning strategies, namely the Exact Q-items Co-occurrence Pruning Strategy (EQCPS) and the Range Q-items Co-occurrence Pruning Strategy (RQCPS), are further adopted and are based on the TQCS structure. EQCPS and RQCPS are used to reduce unpromising exact and unpromising range Q-itemsets respectively. Three effective threshold strategies are adopted to raise the
![]() $min\_util$
threshold to get higher values without the loss of any top-k HUQIs. The first two strategies, RIU and CUD, are applied before the depth-first search method, while the third one is applied during the depth-first search based on the current top-k HUQIs.
$min\_util$
threshold to get higher values without the loss of any top-k HUQIs. The first two strategies, RIU and CUD, are applied before the depth-first search method, while the third one is applied during the depth-first search based on the current top-k HUQIs.
Two modified versions of the proposed algorithm, namely TKQ-RIU and TKQ-CUD, are designed to use the RIU and CUD strategies, respectively. It is observed that TKQ performs better than TKQ-RIU and TKQ-CUD from the benchmark datasets as the value of k is increased. However, for small values of k, the performance of TKQ is quite similar with both modified versions. The reason is that for small values of k, RIU quickly raises
![]() $min\_util$
than CUD, while for large values of k, CUD quickly raises
$min\_util$
than CUD, while for large values of k, CUD quickly raises
![]() $min\_util$
than RIU. Therefore, both strategies can be combined to obtain better results. The performance of TKQ is compared against the state-of-the-art FHUQI-Miner (Nouioua et al., Reference Nouioua, Fournier-Viger, Wu, Lin and Gan2021), and it is found that the FHQI-Miner is generally faster than the proposed algorithm. This is because of the optimal
$min\_util$
than RIU. Therefore, both strategies can be combined to obtain better results. The performance of TKQ is compared against the state-of-the-art FHUQI-Miner (Nouioua et al., Reference Nouioua, Fournier-Viger, Wu, Lin and Gan2021), and it is found that the FHQI-Miner is generally faster than the proposed algorithm. This is because of the optimal
![]() $min\_util$
threshold used by FHUQI-Miner. However, in a real-life scenario, it is difficult for the users to obtain the optimal
$min\_util$
threshold used by FHUQI-Miner. However, in a real-life scenario, it is difficult for the users to obtain the optimal
![]() $min\_util$
threshold; therefore, FHUQI-Miner needs to be executed multiple times to get the optimal
$min\_util$
threshold; therefore, FHUQI-Miner needs to be executed multiple times to get the optimal
![]() $min\_util$
threshold. It is recommended to use TKQ to obtain the desired number of patterns instead of FHUQI-Miner. Moreover, it allows the user to save a significant amount of time to obtain the
$min\_util$
threshold. It is recommended to use TKQ to obtain the desired number of patterns instead of FHUQI-Miner. Moreover, it allows the user to save a significant amount of time to obtain the
![]() $min\_util$
threshold to just get enough patterns.
$min\_util$
threshold to just get enough patterns.
Table 15 describes an overview of the techniques and important strategies which are used in basic utility-list-based top-k HUIM algorithms. Table 16 highlights the pros and cons of all the state-of-the-art basic utility-list-based top-k HUIM algorithms.
Table 15. An overview of the basic utility-list-based top-k HUIM algorithms
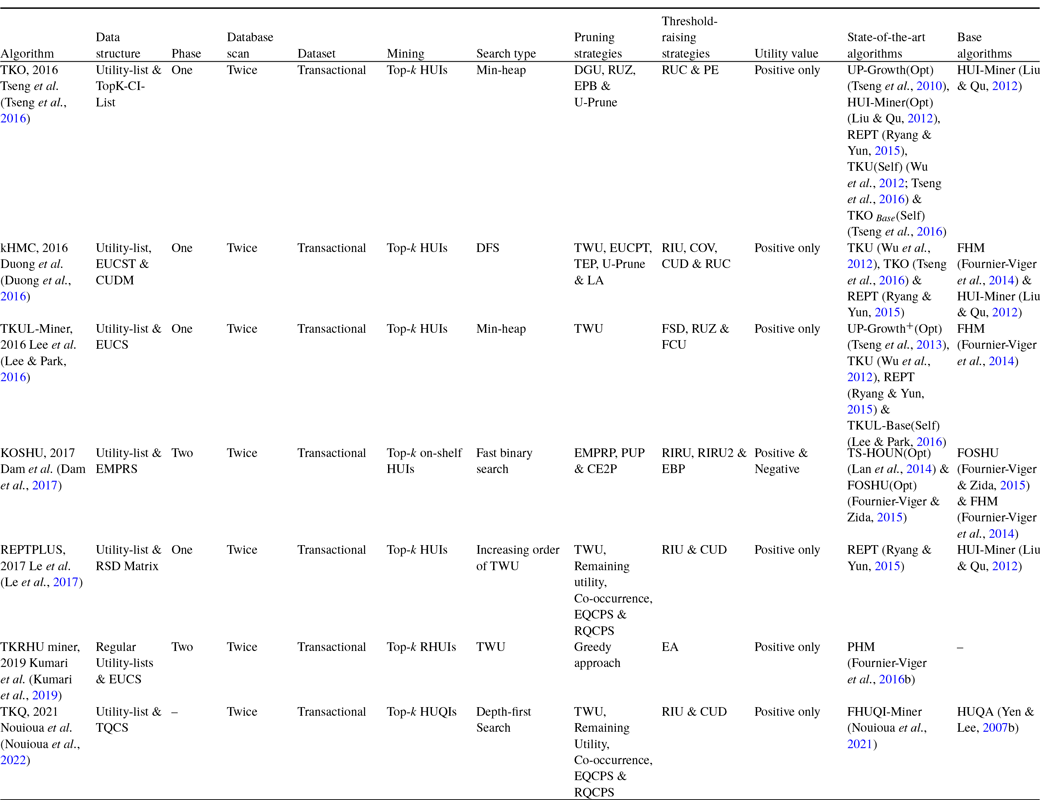
Table 16. Advantages and disadvantages of the basic utility-list-based top-k HUIM algorithms

3.2.2 Extended utility-list-based algorithms
As we have seen previously, one-phase top-k HUIM algorithms (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016; Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) utilise the vertical-list data structure to discover the top-k HUIs. However, they are not very effective in rapidly raising the border threshold in the early stages, especially on dense datasets. In this sub-section, we provide an up-to-date discussion about the extended utility-list-based top-k HUIM algorithms.
Dawar et al. (Reference Dawar, Sharma and Goyal2017) proposed an efficient one-phase vertical dataset based mining algorithm, named Vert
![]() $\_$
top-k_DS (Mining Top-k high utility itemsets over Data Streams), to mine the complete set of top-k HUIs without candidate generations over the sliding window from the data stream. The algorithm keeps the batch-wise TWU of items to smoothly update the TWU of items upon the arrival of the new batch and discard the oldest batch. An inverted-list structure, named iList, an adaption of utility-list (Liu & Qu, Reference Liu and Qu2012), is designed to capture the utility information of an itemset across the sliding windows. It maintains the First-In-First-Out (FIFO) queue to perform the insertion and deletion of batches rapidly. It scans the sliding window twice. During the first scan, it computes the TWU of the items. During the second scan, it sorts the items in each transaction as per the increasing order of TWU and iList for each item. The proposed algorithm Vert
$\_$
top-k_DS (Mining Top-k high utility itemsets over Data Streams), to mine the complete set of top-k HUIs without candidate generations over the sliding window from the data stream. The algorithm keeps the batch-wise TWU of items to smoothly update the TWU of items upon the arrival of the new batch and discard the oldest batch. An inverted-list structure, named iList, an adaption of utility-list (Liu & Qu, Reference Liu and Qu2012), is designed to capture the utility information of an itemset across the sliding windows. It maintains the First-In-First-Out (FIFO) queue to perform the insertion and deletion of batches rapidly. It scans the sliding window twice. During the first scan, it computes the TWU of the items. During the second scan, it sorts the items in each transaction as per the increasing order of TWU and iList for each item. The proposed algorithm Vert
![]() $\_$
top-k_DS adopts a threshold-raising strategy (Zihayat & An, Reference Zihayat and An2014) to calculate the finer threshold for the next sliding window. It calculates the utility of top-k itemsets in the common batches between two sliding windows. It is observed that the vertical mining algorithm works well in the case of the increasing order of TWU values (Liu & Qu, Reference Liu and Qu2012). Therefore, a variant of the proposed algorithm, named Vert
$\_$
top-k_DS adopts a threshold-raising strategy (Zihayat & An, Reference Zihayat and An2014) to calculate the finer threshold for the next sliding window. It calculates the utility of top-k itemsets in the common batches between two sliding windows. It is observed that the vertical mining algorithm works well in the case of the increasing order of TWU values (Liu & Qu, Reference Liu and Qu2012). Therefore, a variant of the proposed algorithm, named Vert
![]() $\_$
top-k naive, is developed to construct the iLists of items from scratch for each sliding window by calculating the sum of the Exact Utility (EU) and Remaining Utility (RU) while scanning the iList data structure.
$\_$
top-k naive, is developed to construct the iLists of items from scratch for each sliding window by calculating the sum of the Exact Utility (EU) and Remaining Utility (RU) while scanning the iList data structure.
The results show the effectiveness of Vert
![]() $\_$
top-k naive over Vert
$\_$
top-k naive over Vert
![]() $\_$
top-k concerning the candidate’s generation and TWU distribution on the dense and sparse datasets. It is observed that the designed approaches outperform the state-of-the-art T-HUDS algorithm (Zihayat & An, Reference Zihayat and An2014) for the varied values of the parameter k, varying window size, computation time, runtime, memory usage, and scalability on dense and sparse datasets. The running time of both approaches grows steadily and linearly, respectively, for sparse and dense datasets. The proposed algorithm performs 20–80 percent and 300–700 percent better on sparse and dense datasets, respectively. However, the efficiency of the proposed algorithm could be further enhanced by reducing the number of intersections of the inverted lists.
$\_$
top-k concerning the candidate’s generation and TWU distribution on the dense and sparse datasets. It is observed that the designed approaches outperform the state-of-the-art T-HUDS algorithm (Zihayat & An, Reference Zihayat and An2014) for the varied values of the parameter k, varying window size, computation time, runtime, memory usage, and scalability on dense and sparse datasets. The running time of both approaches grows steadily and linearly, respectively, for sparse and dense datasets. The proposed algorithm performs 20–80 percent and 300–700 percent better on sparse and dense datasets, respectively. However, the efficiency of the proposed algorithm could be further enhanced by reducing the number of intersections of the inverted lists.
Krishnamoorthy (Reference Krishnamoorthy2019 b) proposesd an efficient algorithm, named THUI (Top-k High Utility Itemset mining), to find top-k HUIs from the dense datasets. A new structure, Leaf Itemset Utility (LIU), based on a triangular matrix, is designed to store the utility information of the contiguous itemsets in a concise form to improve the performance of the mining process. As the space is too small to hold the long contiguous itemsets in the transactions, a hash-map structure is adopted to optimise the search-space. Moreover, a priority queue based data structure is utilised to keep only the top-k utility values. The proposed algorithm THUI adopts two threshold-raising strategies, RIU and RUC, which are described in detail in the literature (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016). The author proposed two new threshold-raising strategies, namely LIU-Exact Utilities (LIU-E) and utility lower-bound estimation (LIU-LB), to effectively raise the threshold. The first threshold strategy, LIU-E, effectively raises the threshold during the initial stage of mining. The second threshold strategy, LIU-LB, stores the information of contiguous itemsets in the LIU matrix to significantly increase the threshold without calculating the real utility values of longer itemsets. THUI adopts the following pruning strategies: (1) The TWU-Prune pruning strategy (Liu et al., Reference Liu and Liao2005) is performed during the initial stage to eliminate non-promising 1-itemsets. (2) The U-Prune pruning strategy (Krishnamoorthy, Reference Krishnamoorthy2017) is performed during the exploration of the search tree. (3) The LA-Prune pruning strategy (Krishnamoorthy, Reference Krishnamoorthy2015) is performed during the traversal of the tree. The proposed approach consists of the following three distinct stages: (1) The TWU values of all 1-itemsets are calculated by scanning the dataset. After that, the RIU strategy is performed to raise the threshold from zero. (2) Unpromising items are pruned based on the TWU-Prune. The ordering of items in the transaction is done according to the ordering heuristic. The LIU matrix is constructed to update the utility values. Finally, a utility list is constructed. First, LIU, and then LIU-LB strategies are performed for raising the threshold. (3) Itemsets are explored in the search-space to mine the top-k HUIs by dynamically raising the threshold in each iteration. The comparative analysis of the proposed algorithm THUI with two-phase algorithms, TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and REPT (Ryang & Yun, Reference Ryang and Yun2015), and with one-phase algorithms, TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) and kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), is shown in Table 17.
Table 17. Comparison of THUI with the state-of-the-art approaches (Krishnamoorthy, Reference Krishnamoorthy2019 b)

The effectiveness of THUI is measured against the state-of-the-art, kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) and TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), for the initial stage of the mining process for the varied values of k, which proves that the proposed algorithm is quite effective to raise the threshold on dense datasets. It can raise the threshold nearly to 100 percent during the initial stages, even for highly dense datasets. Hence, it leads to a significant reduction in candidate generations and improves the overall top-k mining performance. The proposed algorithm THUI is 1–3 orders of magnitude runtime improvement, highly memory efficient, and scalable for the benchmark methods (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) on dense and large datasets. However, the proposed LIU structure could be further optimised to effectively maintain the utility of long itemsets.
Wu and He (Reference Wu and He2018) proposed an effective one-phase method, named TKAU (Top-k high Average-Utility mining), the first of its kind, to find all top-k high average-utility itemsets (HAUIs) from transactional dataset. A novel list data structure, Average-Utility List with Option field (AUO-List), and the construction process are designed to store the information of itemsets in a concise form. The proposed method scans the dataset twice to construct the initial AUO-Lists of 1-itemsets by reorganising the transaction, and then again scans the dataset to build the AUO-Lists of k-itemset
![]() $(k \ge 2)$
by taking the intersection of the AUO-Lists of
$(k \ge 2)$
by taking the intersection of the AUO-Lists of
![]() $(k-1)$
-itemset and 1-itemsets. It mines all the candidate HAUIs without the candidate’s validation process by recursively constructing the AUO-Lists of itemsets of length more than 1. Two novel pruning strategies, namely the Estimated Maximum Utility Pruning strategy (EMUP) and Early Abandoning (EA), are designed to reduce the search-space, avoid costly join operations, and compute the utilities of itemsets. The EMUP is based on the maximum utility information and prunes the unpromising itemsets by avoiding the number of join operations when mining the HAUIs with the AUO-List structure. It is very effective, especially on sparse datasets. The EA strategy terminates the AUO-List construction process of unpromising itemsets in the extension of itemsets using the Local Maximum Average Utility (LMAU) upper bound to significantly minimise the runtime and memory usage. Three threshold-raising strategies, namely RIU, Co-occurrence Average-utility Descending order (CAD), and Exploring the most Promising Branches First (EPBF), are employed for initialising and dynamically adjusting the threshold effectively to reduce the search-space. The RIU strategy (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) computes utilities for all items and is applied after scanning the dataset once. The CAD strategy, a revised version of CUD as in Duong et al. (Reference Duong, Liao, Fournier-Viger and Dam2016), is used to store the average utility of item pairs in the CAD matrix (CADM) structure and is performed after the RIU and second scan. The EPBF is proposed after the construction of initial AUO-Lists of 1-itemsets by extending the itemsets that have a larger average utility value first. Hence, it rapidly raises the threshold to reduce the search-space. The proposed algorithm can reduce up to 90 percent of candidates by using the EPBF strategy. Three versions of TKAU are proposed, namely TKAU
$(k-1)$
-itemset and 1-itemsets. It mines all the candidate HAUIs without the candidate’s validation process by recursively constructing the AUO-Lists of itemsets of length more than 1. Two novel pruning strategies, namely the Estimated Maximum Utility Pruning strategy (EMUP) and Early Abandoning (EA), are designed to reduce the search-space, avoid costly join operations, and compute the utilities of itemsets. The EMUP is based on the maximum utility information and prunes the unpromising itemsets by avoiding the number of join operations when mining the HAUIs with the AUO-List structure. It is very effective, especially on sparse datasets. The EA strategy terminates the AUO-List construction process of unpromising itemsets in the extension of itemsets using the Local Maximum Average Utility (LMAU) upper bound to significantly minimise the runtime and memory usage. Three threshold-raising strategies, namely RIU, Co-occurrence Average-utility Descending order (CAD), and Exploring the most Promising Branches First (EPBF), are employed for initialising and dynamically adjusting the threshold effectively to reduce the search-space. The RIU strategy (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) computes utilities for all items and is applied after scanning the dataset once. The CAD strategy, a revised version of CUD as in Duong et al. (Reference Duong, Liao, Fournier-Viger and Dam2016), is used to store the average utility of item pairs in the CAD matrix (CADM) structure and is performed after the RIU and second scan. The EPBF is proposed after the construction of initial AUO-Lists of 1-itemsets by extending the itemsets that have a larger average utility value first. Hence, it rapidly raises the threshold to reduce the search-space. The proposed algorithm can reduce up to 90 percent of candidates by using the EPBF strategy. Three versions of TKAU are proposed, namely TKAU
![]() $_{EMUP\&EA}$
, TKAU
$_{EMUP\&EA}$
, TKAU
![]() $_{EMUP}$
, and TKAU
$_{EMUP}$
, and TKAU
![]() $_{BothNot}$
, to measure the effectiveness of the designed strategies. The EUMP strategy can reduce numerous candidates, while the EA strategy can further reduce the candidates based on EUMP. EA is quite effective on sparse datasets. TKAU
$_{BothNot}$
, to measure the effectiveness of the designed strategies. The EUMP strategy can reduce numerous candidates, while the EA strategy can further reduce the candidates based on EUMP. EA is quite effective on sparse datasets. TKAU
![]() $_{EMUP\&EA}$
reduces 88 percent more candidates than that of TKAU
$_{EMUP\&EA}$
reduces 88 percent more candidates than that of TKAU
![]() $_{BothNot}$
. The comparative evaluation of these strategies is shown in Table 18.
$_{BothNot}$
. The comparative evaluation of these strategies is shown in Table 18.
Table 18. Comparative analysis of the EMUP and EA strategies of the TKAU algorithm (Wu & He, Reference Wu and He2018)

It is observed that TKAU outperforms the optimal case of the state-of-the-art algorithms HAUI-Tree (Lu et al., Reference Lu, Liu and Wang2014b), HAUI-Miner (Lin et al., Reference Lin, Yang, Fournier-Viger, Wu, Hong, Wang and Zhan2016), and MHAI (Yun & Kim, Reference Yun and Kim2017) for the execution time, number of determining nodes, memory usage, and scalability on dense and sparse datasets. TKAU is 1 to 2 orders of magnitude faster than the optimal cases of HAUI-Tree and HAUI-Miner. TKAU is best suited for real-time applications because of its effectiveness and efficiency. However, TKAU shows less performance than the optimal cases of HAUI-Miner and MHAI in some cases if the proper threshold is set for these existing algorithms.
Gan et al. (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) proposed an effective and scalable exploration approach, named TopHUI (Top-k high utility itemset mining with negative utility), the first of its kind, to find all top-k HUIs with the positive and negative unit profits from the transactional dataset. The proposed algorithm incorporates a vertical list-based structure called Positive-and-Negative Utility-list (PNU-list), as used in FHN (Fournier-Viger, Reference Fournier-Viger, Luo, Yu and Li2014), to keep the information in compact form along with positive and negative utility. The search-space is represented as a set-enumeration tree (Liu & Qu, Reference Liu and Qu2012) to explore all the promising itemsets using the depth-first search. The items are arranged as per the increasing order of Redefined TWU (RTWU) to efficiently prune the search-space (Liu et al., Reference Liu and Liao2005; Liu & Qu, Reference Liu and Qu2012). PNU-list avoids multiple scans and easily computes the total utility, total positive utility, total negative utility, and remaining utility of itemsets in the whole processed dataset. Several pruning strategies, RTWU-prune (Liu et al., Reference Liu and Liao2005), RU-prune (Liu & Qu, Reference Liu and Qu2012; Fournier-Viger, Reference Fournier-Viger, Luo, Yu and Li2014), EUCS-prune (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014), and LA-prune (Fournier-Viger, Reference Fournier-Viger, Luo, Yu and Li2014; Krishnamoorthy, Reference Krishnamoorthy2015), are incorporated to prune the search-space, minimise the runtime, and improve the searching efficiency. These pruning strategies are performed during the different stages of the mining process. RTWU-prune removes unpromising 1-itemsets during the initial stages. RU-prune and EUCS-prune explore the search-space during a depth-first search. LA-prune applies during the construction of the PNU-list. The proposed algorithm TopHUI uses pruning techniques to compute the actual utilities of itemsets and their upper bound on utility in linear time. The threshold-raising strategies, RIU (Ryang & Yun, Reference Ryang and Yun2015), RTU (Ryang & Yun, Reference Ryang and Yun2015), Raising threshold based on RTWU (RTWU), and RUC (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), are incorporated to quickly raise the minimum-utility threshold.
Two variants are designed to measure the effectiveness of the proposed algorithm. The basic version, TopHUI
![]() $_{Basic}$
, incorporates only threshold-raising strategies, while TopHUI includes both pruning and threshold-raising strategies. It is observed that TopHUI outperforms the basic version TopHUI
$_{Basic}$
, incorporates only threshold-raising strategies, while TopHUI includes both pruning and threshold-raising strategies. It is observed that TopHUI outperforms the basic version TopHUI
![]() $_{Basic}$
in terms of search-space, unpromising candidates, and dataset scans. The reason is that the pruning strategies used significantly minimise the number of dataset scans and reduce the number of candidates. TopHUI outperforms the state-of-the-art THUI (Krishnamoorthy, Reference Krishnamoorthy2019
b) in terms of execution time and memory usage on dense and sparse datasets.
$_{Basic}$
in terms of search-space, unpromising candidates, and dataset scans. The reason is that the pruning strategies used significantly minimise the number of dataset scans and reduce the number of candidates. TopHUI outperforms the state-of-the-art THUI (Krishnamoorthy, Reference Krishnamoorthy2019
b) in terms of execution time and memory usage on dense and sparse datasets.
Nouioua et al. (Nouioua et al., Reference Nouioua, Wang, Fournier-Viger, Lin and Wu2020) proposed a cross-level approach, named TKC (Top-k Cross-level high utility itemset miner), to discover all top-k cross-level HUIs. It adopts depth-first search and optimisation to enhance mining performance. The cross-level HUIs consist of generalised and non-generalised items with high utilities. The higher items in the taxonomy are traversed before the lower items to prune the specialisation of generalised itemsets having lower upper-bound values on the utilities. TKC explores the search-space by considering itemsets having a single item from the taxonomy. Then, it repeatedly applies two types of itemsets expansion, namely Joined-based and Tax-based (Fournier-Viger et al., Reference Fournier-Viger, Wang, Lin, Luna, Ventura, Fujita, Fournier-Viger, Ali and Sasaki2020), to discover the other itemsets. The proposed algorithm utilises a list-based structure, named tax-utility-list, as used in CLH-Miner (Fournier-Viger et al., Reference Fournier-Viger, Wang, Lin, Luna, Ventura, Fujita, Fournier-Viger, Ali and Sasaki2020), to maintain information about each pattern in the mining process. It rapidly computes the utility and upper bound on itemsets utility and their extensions without scanning the dataset multiple times. The tax-utility-list is constructed for each explored itemset while searching the cross-level itemsets. It can extend the utility list as used in Qu et al. (Reference Qu, Liu and Fournier Viger2019) with additional taxonomy details. The tax-utility-lists of larger itemsets are built using the simple join operations of smaller itemsets by a modified construct procedure (Cagliero et al., Reference Cagliero, Chiusano, Garza and Ricupero2017). Although the structure is efficient for computing the utility of an itemset. However, it is impractical to conduct an exhaustive search to take into account all the transitive extensions of single items, especially if there are an excessive number of items. To deal with this issue, two pruning strategies (Fournier-Viger et al., Reference Fournier-Viger, Wang, Lin, Luna, Ventura, Fujita, Fournier-Viger, Ali and Sasaki2020) are utilised to efficiently discover the cross-level HUIs. The first strategy is based on the Generalised-Weighted Utilization (GWU) measure, a generalisation of TWU as used in Liu et al. (2005), while the second strategy is based on the notion of Remaining Utility (RU) (Qu et al., Reference Qu, Liu and Fournier Viger2019). The proposed algorithm incorporates an optimisation by raising the threshold with the utility of (generalised) items to enhance the mining performance.
It is observed that the designed algorithm TKC optimizes the performance on two real-time customer datasets (Fruithut and Liquors) with taxonomy information in terms of the tax-based and join-based extension count, execution time, memory consumption, and scalability. TKC performs better than the state-of-the-art CLH-Miner (Fournier-Viger et al., Reference Fournier-Viger, Wang, Lin, Luna, Ventura, Fujita, Fournier-Viger, Ali and Sasaki2020) for the optimal minimum-utility threshold for all values of k. However, TKC is slightly faster and consumes more memory than CLH-Miner. But the proposed algorithm still has advantages as it obtains the exact top-k cross-level HUIs and spends less time to get the optimal threshold to discover promising top-k patterns.
Table 19 shows a detailed overview of extended utility-list-based top-k HUIM algorithms. Table 20 depicted the pros and cons of extended utility-list-based top-k HUIM algorithms.
Table 19. An overview of the extended utility-list-based top-k HUIM algorithms
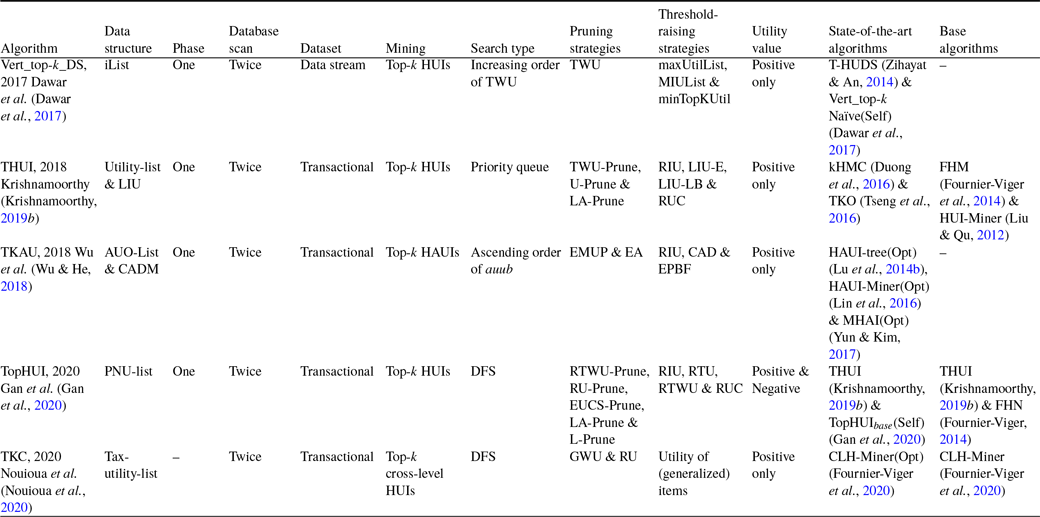
Table 20. Advantages and disadvantages of the extended utility-list-based top-k HUIM algorithms

3.3 Other top-k HUIM algorithms
In real-time applications, the profit of recommended itemsets is measured by using only the utility values of the itemsets. However, the diversity of intended itemsets is equally important for the satisfaction of the users. Traditional top-k HUIM algorithms (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Ryang & Yun, Reference Ryang and Yun2015; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016; Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) cannot mine the diversify top-k HUIs. This problem can be solved by using multi-objective optimisation that considers both measure, utility, and coverage to mine diversified top-k HUIs (Zhang et al., Reference Zhang, Yang, Wu, Cheng, Xie and Lin2019). Moreover, the traditional top-k HUIM algorithm can work only for small or medium-sized data that can be kept completely in memory. They do not perform well on extremely large data sets. There is a need to design an efficient algorithm that can efficiently work in cases of extremely large dataset (Han et al., Reference Han, Liu, Li and Gao2021). To deal with this issue, the concept of cross-entropy (de Boer et al., Reference de Boer, Kroese, Mannor and Rubinstein2004) is utilised to estimate the probabilities of the promising candidates. An efficient top-k HUIM approach is proposed to find top-k using combinatorial optimisation (Song et al., Reference Song, Liu and Huang2020). In this sub-section, we provide a brief analysis of the other data structure based top-k HUIM algorithms.
There is a recent trend in increasing Recommender Systems (RS) because they allow customers to quickly analyse their purchases without wasting time. These systems allow retailers to easily analyse their profits. However, most RS fails to optimise revenue. To meet these challenges, Yang et al. (Reference Yang, Xu, Jones and Samatova2017) defined the problem of the utility of recommendation sets and proposed an efficient algorithm named RAOTK (Adaptive Online Top-K high utility itemsets mining model) that provides real-time utility-based recommendation to optimise the revenue of itemsets on the streaming data. The RAOTK algorithm utilises three strategies, namely Itemsets normalization by utility (INU), Weighted random selection (WRS), and Personalized strategy (PS), that are used to generate the recommendation candidates. Three variants of the proposed algorithm, namely RAOTK with Ratings (RAOTK-R), RAOTK with Frequency (RAOTK-F), and Hybrid RAOTK with ratings and frequency (RAOTK-H), are designed to provide the overall set of utility-based recommendation systems. RAOTK-R incorporates the utility-based rating (UR) into RAOTK, which improves the performance of the utility-based recommendation system. It also uses the UR-guided selection strategy to generate recommendation candidates with the probability method. It uses a Modified personalized strategy (MPS) based on UR to control the parameters. RAOTK-F incorporates the frequency information into utility-based recommendations. It uses a Utility-based frequency (UF) and UF-guided selection strategy that improves the performance of the system. RAOTK-H combines the features of both RAOTK-R and RAOTK-F that incorporate the Hybrid Utility Evaluation (HUE) and a HUE-guided selection strategy to improve the performance of the system. The authors also provide an effective method, named Online consumers’ Willingness to Pay (OWP), to consider the buying power of customers to make the system more accurate and personalized. The RAOTK algorithm utilises the user’s purchase history (PH) to achieve better accuracy. PH works in the following two ways: first, it combines with the top-k HUIs pool, and then, PH is inserted into the online transaction stream to obtain the personalised recommendation.
To measure the effectiveness of the revenue optimisation, the proposed algorithm RAOTK is compared with the state-of-the-art G-Greedy (Lu et al., Reference Lu, Liu and Wang2014c), TopR (Top-rating) recommends (Gantner et al., Reference Gantner, Rendle, Freudenthaler and Schmidt-Thieme2011), and TopF (Top-frequency) recommends (Thanh Lam & Calders, Reference Thanh Lam and Calders2010). It is observed that RAOTK generates 20 percent more revenue as compared to G-Greedy. It is about 2–3 times better than TopR and TopF. There is a significant difference in the performance of RAOTK-R and RAOTK-F because of the different preferences of the users. The OWP model gains effectiveness by about 10–20 percent in most cases as compared to the benchmark datasets.
The existing bio-inspired algorithms (Holland, Reference Holland1975; Kennedy & Eberhart, Reference Kennedy and Eberhart1995; Yang, Reference Yang2011) maintain the current optimal values in the next population, which gives the undesired results because of the non-uniformity of the distribution of HUIs. To resolve this issue, Song & Huang (Reference Song and Huang2018) proposed an efficient algorithm, named Bio-HUIF (Bio-inspired based HUIM framework), to mine top-k HUIs. It utilises a roulette wheel selection procedure to find the optimal values for the next population. The authors proposed three novel algorithms, namely Bio-HUIF-GA, Bio-HUIF-PSO, and Bio-HUIF-BA, based on GA (Genetic algorithm) (Holland, Reference Holland1975), PSO (Particle swarm optimization) (Kennedy & Eberhart, Reference Kennedy and Eberhart1995), and BA (Bat Algorithm) (Yang, Reference Yang2011), respectively. The three strategies, namely bitmap dataset representation (Song et al., Reference Song, Liu and Li2014), promising encoding vector checking (PEVC), and bit difference sets, are utilised to speed up the process of discovering the top-k HUIs. In the first scan, the 1-HTWUIs are calculated based on the TWU model (Liu et al., Reference Liu and Liao2005). After this, a bitmap representation is formed by using PEVC. Finally, the complete set of HUIs is obtained. The experiments show the effectiveness of the proposed algorithm over the existing bio-inspired algorithms, HUPE
![]() $_{umu}$
-GRAM (Kannimuthu & Premalatha, Reference Kannimuthu and Premalatha2014) and HUIM-BPSO (Lin et al., Reference Lin, Yang, Fournier-Viger, Hong and Voznak2017), and two state-of-the-art HUIM algorithms, IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009) and UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), regarding the runtime, number of discovered HUIs, and converging speed on the benchmark datasets.
$_{umu}$
-GRAM (Kannimuthu & Premalatha, Reference Kannimuthu and Premalatha2014) and HUIM-BPSO (Lin et al., Reference Lin, Yang, Fournier-Viger, Hong and Voznak2017), and two state-of-the-art HUIM algorithms, IHUP (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009) and UP-Growth (Tseng et al., Reference Tseng, Wu, Shie and Yu2010), regarding the runtime, number of discovered HUIs, and converging speed on the benchmark datasets.
The notion of coverage (Zuo et al., Reference Zuo, Gong, Zeng, Ma and Jiao2015) is used to measure the diversification of top-k patterns. By using the concepts of relative utility and coverage, the users can get both high (relative) utility and diversified patterns. However, both of these concepts conflict with each other, meaning that high utility results in low coverage and vice versa. To address the above issues, Zhang et al. (Reference Zhang, Yang, Wu, Cheng, Xie and Lin2019) proposed an indexed set-based representation MOE algorithm, named ISR-MOEA (Indexed Set Representation-based Multi-Objective Evolutionary Approach), the first of its kind, to mine diversified top-k HUIs to improve the user’s satisfaction. The ISR-MOEA is implemented by using the designed indexed set-based representation scheme and the frameworks of MOEA/D (Zhang & Li, Reference Zhang and Li2007), NSGA-II (Deb et al., Reference Deb, Pratap, Agarwal and Meyarivan2002), and SPEA-II (Zitzler et al., Reference Zitzler, Laumanns and Thiele2001) to guarantee a better trade-off between the convergent and diverse populations during the evolution process. The framework of ISR-MOEA consists of the following three steps: (1) population initialization, (2) population evolution, and (3) population selection. A new population initialization strategy is proposed, based on NSGA-II (Deb et al., Reference Deb, Pratap, Agarwal and Meyarivan2002), to generate diversified and useful solutions. Two effective evolutionary operators, namely crossover and mutation, are proposed to accelerate the convergence of the population.
Three variants of the proposed algorithms, namely ISR-MOEA (Support), ISR-MOEA (Utility), and ISR-MOEA (Random), are designed to measure the effectiveness of ISR-MOEA. It is observed that ISR-MOEA with both utility and support performs better than ISR-MOEA (support) or ISR-MOEA (utility), while ISR-MOEA (random) cannot coverage all the possible generated solutions. For example, on chess and OnlineRetail datasets, ISR-MOEA can converge very quickly within 100 generations. The ISR-MOEA outperforms the state-of-the-art and their variants, namely TKO, TKO-Greedy, PSO-Miner, BGSA-Miner, SSDP-Miner, ISR-NSGA2, ISR-SPEA2, ISR-SPEA2, ISR-MOEA(Support), ISR-MOEA(Utility), and ISR-MOEA(Random), in terms of the population size, neighbour size, generated patterns, and mutation probability on the large and sparse datasets. ISU-MOEA with the MOEA/D framework provides better results than those obtained using NSGA-II or SPEA-II. The proposed ISR-MOEA provides multiple recommendations simultaneously in a single run to make the decision quickly.
Lin et al. (Reference Lin, Wu, Huang and Tseng2019) proposed an algorithm, named PKU (Parallel Top-K High Utility Itemset Mining), the first of its kind, to mine the top-k HUIs parallel mining on the Spark in-memory environment. The proposed algorithm consists of the following three stages: (1) Pre-Evaluation in Parallel (PEP) (2) Reorganize Transactions in Parallel (RTP); (3) Mining Patterns in Parallel (MPP). PEP performs the following two steps: (1) During the first step, it finds all the items and their corresponding utilities in a MapReduce pass. (2) During the second step, it finds a few 2-itemsets and their partial utilities in the MapReduce pass. RTP performs the following two steps: (1) During the first step, it finds all the items along with TWUs by using the MapReduce pass. (2) During the second step, it uses TWDCP (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) to prune the unpromising itemsets. MPP performs the following two steps: (1) During the first step, it uses a pattern-growth method to find top-k HUIs using the MapReduce iterations. (2) During the second step, it sorts all the items in the PKHUI List (PKL) according to the decreasing order of their utilities. The novel pruning strategies, namely Discarding Local Unpromising Items in Parallel (DLUP) and Merge Conditional Transactions in Parallel (MCTP), are proposed to reduce the redundant unpromising candidates and size of conditional datasets, resulting in a significant decrease in the runtime and memory consumption in each MapReduce pass. The threshold-raising strategies are proposed to effectively raise the border
![]() $min\_util$
threshold by using the dynamically adjusted internal variable. PKU mines the complete set of top-k HUIs after the mining process. The proposed algorithm performs well as compared to the optimal value of the state-of-the-art TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), HUI-Miner (Liu & Qu, Reference Liu and Qu2012), and PHUI-Growth (Lin et al., Reference Lin, Wu, Tseng, Cao, Lim, Zhou, Ho, Cheung and Motoda2015) in terms of communication cost, fault tolerance, and scalability. The characteristics of these algorithms are shown in Table 21. The experimental results show that for
$min\_util$
threshold by using the dynamically adjusted internal variable. PKU mines the complete set of top-k HUIs after the mining process. The proposed algorithm performs well as compared to the optimal value of the state-of-the-art TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), HUI-Miner (Liu & Qu, Reference Liu and Qu2012), and PHUI-Growth (Lin et al., Reference Lin, Wu, Tseng, Cao, Lim, Zhou, Ho, Cheung and Motoda2015) in terms of communication cost, fault tolerance, and scalability. The characteristics of these algorithms are shown in Table 21. The experimental results show that for
![]() $k \le 100$
, TKU and HUI-Miner perform better than PKU. The reason is that PKU incurs additional communication costs among nodes. However, as the value of k increases, PKU works better than the optimal cases of TKU, HUI-Miner, and PHUI-Growth because the benchmark algorithms cannot handle the increasing overhead, while the proposed algorithm has features of the parallel framework that significantly reduce the overhead. For
$k \le 100$
, TKU and HUI-Miner perform better than PKU. The reason is that PKU incurs additional communication costs among nodes. However, as the value of k increases, PKU works better than the optimal cases of TKU, HUI-Miner, and PHUI-Growth because the benchmark algorithms cannot handle the increasing overhead, while the proposed algorithm has features of the parallel framework that significantly reduce the overhead. For
![]() $ k = 10\,000$
, PKU is 50 times better than TKU. It is observed that PKU with MCTP performs better than PKU without MCTP. The runtime of PKU with MCTP is approximately 90 times less than that of PKU without MCTP to complete the mining process. The runtime of PKU is about 4–5 times better than PHUI-Growth.
$ k = 10\,000$
, PKU is 50 times better than TKU. It is observed that PKU with MCTP performs better than PKU without MCTP. The runtime of PKU with MCTP is approximately 90 times less than that of PKU without MCTP to complete the mining process. The runtime of PKU is about 4–5 times better than PHUI-Growth.
Table 21. Characteristics of TKU, HUI-Miner, PHUI-Growth, and the PKU algorithm (Lin et al., Reference Lin, Wu, Huang and Tseng2019)

Han et al. (Reference Han, Liu, Li and Gao2021) proposed a baseline algorithm (BA) with Apriori-like level-wise execution mode to deal with very large data from the transactional dataset. It significantly reduces the number of scans and numerous candidates; however, it suffers from high computation and I/O costs. Therefore, the authors proposed an efficient prefix-partitioning-based approach, named PTM (Prefix-partitioning-based Top-k high utility itemset Mining), to find the top-k HUI on the very large data from the transactional dataset. PTM has the following features: (1) generates all the top-k HUIs, (2) maintains the entire data in memory, and (3) reduces the processing cost. The prefix-based partition is applied only once using the sequential scan, computes the utility of an itemset in one partition only, and significantly accelerates the mining process. PTM uses pre-constructed concise data structures, namely Utility Information in Partition (UIP
![]() $_a$
), UIP information of Offset and Maximum twu (UOM(mtwu, offs)), and copy of UIP (UIP
$_a$
), UIP information of Offset and Maximum twu (UOM(mtwu, offs)), and copy of UIP (UIP
![]() $_{sor}$
), to skip most of the partitions that do not consist of the top-k HUIs, resulting in saving computational cost and I/O cost-effectively. The elements in UIP
$_{sor}$
), to skip most of the partitions that do not consist of the top-k HUIs, resulting in saving computational cost and I/O cost-effectively. The elements in UIP
![]() $_a$
are arranged in the decreasing order of TWU by performing a single scan. UOM(mtwu, offs) consists of the offset of the first element of UIP
$_a$
are arranged in the decreasing order of TWU by performing a single scan. UOM(mtwu, offs) consists of the offset of the first element of UIP
![]() $_a$
in UIP and the maximum TWU value among UIP
$_a$
in UIP and the maximum TWU value among UIP
![]() $_a$
. PTM keeps UIP
$_a$
. PTM keeps UIP
![]() $_{sor}$
in the decreasing order of utility values. PTM processes the partitions in the selection order of average transaction utility to rapidly raise the border optimal minimum utility threshold. Therefore, it significantly prunes the search-space to enhance mining performance. The full-suffix-utility-based sub-tree pruning rule is also designed to reduce the exploration search-space, thereby accelerating the in-memory processing further.
$_{sor}$
in the decreasing order of utility values. PTM processes the partitions in the selection order of average transaction utility to rapidly raise the border optimal minimum utility threshold. Therefore, it significantly prunes the search-space to enhance mining performance. The full-suffix-utility-based sub-tree pruning rule is also designed to reduce the exploration search-space, thereby accelerating the in-memory processing further.
It is observed that PTM works better than the baseline algorithm (BA) concerning the number of transactions, result size, number of items, and average transaction width on the massive data from the transactional datasets. PTM maintains 9.32 times more transactions as compared to the original dataset. Moreover, PTM consists of six times more items in the prefix-based partition than the original dataset. However, it occupies a large space overhead. PTM is 48.271 times faster, 429.798 fewer candidates, and 4.634 times less I/O cost than that of baseline BA. PTM performs better than the state-of-the-art TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), THUI (Krishnamoorthy, Reference Krishnamoorthy2019 b), and TONUP (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018) for the runtime and number of promising itemsets on the small and medium-size data from the real and synthetic datasets. However, PTM incurs higher I/O costs than the existing algorithms. It does not perform well on highly dense datasets.
To avoid the constant threshold-raising, Song et al. (Reference Song, Liu and Huang2020) adopted the heuristic method of cross-entropy (CE) method (de Boer et al., Reference de Boer, Kroese, Mannor and Rubinstein2004), and proposed the novel efficient algorithm, named TKU-CE (Top-k high Utility mining based on Cross-Entropy method), the first of its kind, to mine the top-k HUIs. CE solves combinatorial optimization problems (COP) to estimate the probabilities of a complex event in stochastic networks. The proposed algorithm follows the COP methodology to determine the top-k HUIs. TKU-CE adopts the utility value by using a bitmap item information representation structure. It uses the bitmap cover to represent the itemset, in that one bit is assigned for each transaction in the dataset. It does not require additional tree or list structures to modify the actual information. It avoids the threshold-raising and pruning strategies of the existing methods to get the intended results.
It is observed that TKU-CE performs better than the state-of-the-art TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) for execution time, memory usage, and accuracy on the benchmark datasets. On the T25I100D5k dataset, TKU-CE is 8.70 times and 1 order of magnitude faster than that of TKU and TKO when k is set to be (
![]() $ 20 \le k \le 100 $
). Similarly, on the T35I100D7k dataset, TKU-CE is 3 orders of magnitude faster than TKO when k is set to be (
$ 20 \le k \le 100 $
). Similarly, on the T35I100D7k dataset, TKU-CE is 3 orders of magnitude faster than TKO when k is set to be (
![]() $ 3 \le k \le 11 $
), while TKU fails to terminate for these values of k. On the chess dataset, TKU-CE is 4.43 times faster than TKO when k is set to be (
$ 3 \le k \le 11 $
), while TKU fails to terminate for these values of k. On the chess dataset, TKU-CE is 4.43 times faster than TKO when k is set to be (
![]() $ 20 \le k \le 100 $
), while TKU runs out of memory for these values of k. TKU-CE consumes 2.69 times, 2.75 times, and 4.92 times less memory than TKO on the Chess, T25I100D5k, and Connect datasets, respectively. However, the performance evaluation of TKU-CE is compared only with TKU and TKO on two real and two synthetic datasets, but there are many other efficient algorithms available in the literature.
$ 20 \le k \le 100 $
), while TKU runs out of memory for these values of k. TKU-CE consumes 2.69 times, 2.75 times, and 4.92 times less memory than TKO on the Chess, T25I100D5k, and Connect datasets, respectively. However, the performance evaluation of TKU-CE is compared only with TKU and TKO on two real and two synthetic datasets, but there are many other efficient algorithms available in the literature.
Heuristic approaches can explore the extremely large search-space to obtain optimal solutions. Song et al. (Reference Song, Li, Huang, Tan and Shi2021) proposed two cross-entropy (CE)-based approaches, namely TKU-CE and TKU-CE+ (Heuristically mining the Top-K high Utility itemsets with Cross-Entropy optimization). TKU-CE+ is an extended version of TKU-CE which mines the top-k rules heuristically. TKU-CE uses bitmap representation to compute the utility values of the intended itemsets. The dataset is transformed into a bitmap to encode each itemset in a binary vector (or itemset vector (IV)). It adopts CE optimisation to model the top-k HUIM problem. The probability vector is initialised randomly to iteratively discover top-k HUIs. The improved TKU-CE+ further improves the performance of TKU-CE by considering the following three observations: (1) Non-promising items can be avoided during the early stage to minimise the length of item vectors. It significantly prunes the search-space, thereby speeding up the mining process. (2) The performance of the mining process can be significantly enhanced by considering only the promising item vectors. (3) Population diversity can be used to improve the diversity of each sample to obtain the intended results. TKU-CE+ proposes several strategies to improve mining performance. The critical utility value-based pruning strategy, named CUV-based pruning, is designed to reduce the unpromising itemsets in the early stages. The size of an elite sample is gradually increased as the number of iterations increases. Therefore, a sample refinement (SR) strategy is proposed to reduce the search-space and computational cost. Another strategy, named smoothing mutation, is proposed to increase the diversity of the item vectors in each iteration, thereby leading to a reduction in the number of generated item vectors. TKU-CE+ outperforms TKU-CE in the following ways: (1) The CUV strategy prunes the itemsets in the early stages, resulting in a reduction in the length of item vectors and probability vectors. (2) The SR strategy considers only the elite item vectors in each iteration, thus reducing the computational cost. (3) A smooth mutation strategy generates more diversified item vectors.
TKU-CE+ outperforms the state-of-the-art TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), and kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) for the runtime and memory usage. It is observed that TKU-CE and TKU-CE+ are always faster than TKU and TKO. In most cases, they are faster compared to kHMC, especially on synthetic datasets. However, TKU-CE+ consumes 27.57 percent more memory than kHMC on the Chainstore dataset. TKU-CE+ is faster than TKU-CE because of CUV, SR, and smoothing mutation strategies. TKU-CE and TKU-CE+ consume almost constant memory because both algorithms do not use additional data structures or threshold-raising strategies. TKU-CE+ achieves a greater reduction in the length of item vectors than TKU-CE because of the CUV strategy, especially on real datasets. Bit Edit Distance (BED) (Song & Li, Reference Song, Li, Yang, Wang, Islam and Zhang2020) is used to check the effectiveness of the smoothing mutation strategy. The Maximal BED (Max_BED) and Average BED (Ave_BED) are used, respectively, to find the greatest and average diversity of all pairs of item vectors. It is observed that TKU-CE+ discovers more Max_BED and Ave_BED than TKU-CE on benchmark datasets. It means that the smoothing mutation strategy improves the diversity of samples to a large extent, thus increasing the execution speed and reducing memory consumption. TKU-CE+ and TKU-CE achieve 100 percent accuracy in 68 percent and 72 percent cases, respectively, in most of the datasets. Although TKU-CE+ mines top-k HUIs within a limited time, it incurs high computation costs.
Pallikila et al. (Reference Pallikila, Veena, Kiran, Avatar, Ito, Zettsu and Reddy2021) proposed a novel algorithm, named TKSHUIM (Top-K Spatial High Utility Itemset Miner), that mines the top-k SHUIs from the spatiotemporal datasets. The proposed algorithm deals with both raster and vector data of spatial items that may be of any size and shape. It uses the depth-first search to find all top-k SHUIs in just a single database scan. A novel utility constraint, named Dynamic utility constraint (dMinUtil), is designed to significantly prune the search-space by utilising the greedy approach. The Min-Heap data structure is used to store the top-k candidates SHUIs because it is easy to update the dMinUtil as the utility of itemset presents at the root node of Min-Heap. The pruning strategy, named Probable maximum utility (PMU), is designed to consider both utility and distance constraints to prune the search-space. The proposed algorithm uses two utility and neighborhood-based pruning strategies, namely Neighborhood sub-tree utility (NSTU) and Neighborhood local utility (NLU), with respect to the sub-tree of an itemset in the search enumeration tree. Five novel threshold strategies, namely Raising dMinUtil using 1-itemsets (RD-1), Raising dMinUtil using 2-itemsets (RD-2), Raising dMinUtil using closed spatial itemsets (RD-3), Raising dMinUtil using utility lower-bound (RD-4), and Raising dMinUtil using exact utility (RD-5), effectively raise the dMinUtil threshold. The first four strategies are employed during the initial phase, while the fifth strategy is employed in the recursive mining phase. An upper triangular matrix, named Utility matrix (UM), is created by using the neighbouring lists of each item by scanning the spatial dataset. The R-tree structure (Guttman, Reference Guttman1984) is used to store the neighbouring lists of each itemset. RD-1 and RD-2 threshold-raising strategies use the UM to calculate the exact utilities of 1-itemsets and 2-itemsets, respectively, that are used to effectively raise the dMinUtil. They use the top-k Min-Heap (top-k MH) to store the non-zero values of 1-itemsets and 2-itemsets in the UM. RD-3 and RD-4 threshold-raising strategies generate the Closed spatial itemsets (CSIs). CSIs are the longest itemsets that are produced by an item in such a way that each pair of items in the generated itemsets exists in the neighbour lists. RD-3 calculates the exact utilities of all generated CSIs, and if the value of CSIs is no less than dMinUtil, then they are added to the top-k MH to effectively raise the dMinUtil. On the other hand, RD-4 uses the utility lower-bound (ULB), and if the ULB of an itemset is no less than dMinUtil, it is added to top-k MH to effectively raise the dMinUtil. RD-5 uses a depth-first search during the recursive mining phase of the proposed algorithm. It calculates the exact utility of an itemset, and if this utility is no less than dMinUtil, then it is added to the top-k MH to effectively raise the dMinUtil. The proposed algorithm consists of three stages: (1) In the first stage, the spatial dataset is scanned to compute the PMU, UM, and utility of CSIs. Then, RD-1, RD-2, RD-3, and RD-4 threshold-raising strategies are applied to raise the dMinUtil. (2) In the second stage, it first prunes the PMU values of items that are no more than dMinUtil, then it scans the dataset to sort the itemsets according to the ascending order of their PMU value. (3) In the third stage, it recursively explores itemsets by using a depth-first search.
The experimental results show that the proposed algorithm TKSHUIM performs well compared to the state-of-the-art THUI (Krishnamoorthy, Reference Krishnamoorthy2019 b) and optimal case of SHUI-Miner (Kiran et al., Reference Kiran, Zettsu, Toyoda, Fournier-Viger, Reddy and Kitsuregawa2019) in terms of runtime and memory consumption from the benchmark datasets. It is observed that the use of pruning and threshold-raising strategies effectively enhances mining performance. Two case studies are also carried out to show the usefulness of the proposed algorithm. The first case study is performed to identify the top-k COVID hot spots in Tokyo, while the second case study is performed to identify the top-k global heavy rainfall regions. The experiments show significant results in both case studies.
The existing top-k HUIM algorithms (Wu et al., Reference Wu, Shie, Tseng and Yu2012; Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) show poor performance when the number of distinct items is significantly increased in the database. To address this issue, the heuristic-based bio-inspired evolutionary computation (EC) algorithm (Song & Li, Reference Song, Li, Yang, Wang, Islam and Zhang2020) is proposed, which obtain optimal solutions in the large search-space. However, they consume a high amount of time to find HUIs. To address this issue, Pham et al. (Reference Pham, Komnková Oplatková, Huynh and Vo2022a) proposed an efficient Binary particle swarm optimization (BPSO)-based algorithm, named TKO-BPSO (top-k high utility itemset mining in One phase based on Binary Particle Swarm Optimization), to effectively mine top-k HUIs. The utility-list structure (Liu & Qu, Reference Liu and Qu2012) is used to store the utility information of the itemsets in the database, which significantly reduces database scans. A threshold-raising strategy named RUC (Strategy to Raise the threshold by the Utilities of Candidates) is used to raise the border threshold, which effectively prunes the search-space. A sigmoid function is also adopted to update the process of the particles, which significantly reduces the combinatorial problems in HUIM. The experiments prove that the proposed algorithm TKO-BPSO outperforms the state-of-the-art algorithms TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) in terms of runtime and memory usage on the benchmark datasets.
Pham et al. (Reference Pham, Komnková Oplatková, Huynh and Vo2022b) proposed an efficient bio-inspired algorithm named TKO-HUIM-PSO (mining top-k high utility itemset in One phase based on a HUIM Framework of Particle Swarm Optimization) to mine top-k HUIs. It uses the bitmap data representation to check the promising encoding vector that speeds up the discovery process to find HUIs. Furthermore, it applies roulette wheel selection to probabilistically select the explored HUIs, which improves the diversity of the populations. A pruning strategy named PEVC (Promising encoding vector check) is designed to prune the search-space, thereby increasing the mining performance. The experimental results prove that the proposed algorithm performs well as compared to the state-of-the-art algorithms TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) and TKO-BPSO algorithm (Pham et al., Reference Pham, Komnková Oplatková, Huynh and Vo2022a) regarding runtime and memory consumption on the benchmark datasets.
The existing HUIM algorithms (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Lee2009; Liu et al., Reference Liu and Liao2005; Tseng et al., Reference Tseng, Shie, Wu and Yu2013) suffer from long execution times and high memory consumption, especially in the case of the large search-space. Moreover, these algorithms work only in the case of positive utility. However, in real-time applications, negative utility, real unit profits, and integers also exist. To resolve these issues, (Luna et al., 2023) proposed an efficient algorithm named TKHUIM-GA (top-k High Utility Itemset Mining through Genetic Algorithms) to mine top-k HUIs. It utilises two data representations, namely vertical and horizontal data representations, to minimise runtime and memory usage, thereby increasing the mining speed. The vertical data representation provides fast access to the utilities associated with each transaction, while the horizontal data representation uses the hashing function to speed up the mining process. The proposed algorithm efficiently works on positive utility, negative utility, real unit profits, and integer value because it only considers the items.
The experimental results show that the proposed algorithm TKHUIM-GA outperforms the existing bio-inspired algorithms, namely HUIM-GA (Kannimuthu & Premalatha, Reference Kannimuthu and Premalatha2014), HUIM-BPSO (Lin et al., Reference Lin, Yang, Fournier-Viger, Wu, Hong, Wang and Zhan2016), HUIM-GA-tree (Lin et al., Reference Lin, Yang, Fournier-Viger, Wu, Hong, Wang and Zhan2016), HUIM-BPSO-tree (Lin et al., Reference Lin, Yang, Fournier-Viger, Wu, Hong, Wang and Zhan2016), HUIF-PSO (Song & Huang, Reference Song and Huang2018), HUIF-GA (Song & Huang, Reference Song and Huang2018), HUIF-BA (Song & Huang, Reference Song and Huang2018), HUIM-ABC (Song et al., Reference Song, Li, Huang, Tan and Shi2021), HUIM-SPSO (Song & Li, Reference Song, Li, Yang, Wang, Islam and Zhang2020), HUIM-AF (Song et al., Reference Song, Li, Huang, Tan and Shi2021), HUIM-HC (Nawaz et al., Reference Nawaz, Fournier-Viger, Yun, Wu and Song2021), and HUIM-SA (Nawaz et al., Reference Nawaz, Fournier-Viger, Yun, Wu and Song2021), two heuristic-based algorithms, namely TKU-CE (Song et al., Reference Song, Liu and Huang2020) and TKU-CE+ (Song et al., Reference Song, Li, Huang, Tan and Shi2021), and two deterministic algorithms, namely TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), regarding runtime and memory usage on the benchmark datasets. It is observed that the proposed algorithm finds the best optimal solution in most of the cases. However, it is uncertain to find the best solutions because it works heuristically. Table 22 describes the overview of other data-structure based top-k HUIM algorithms. Table 23 highlights the pros and cons of all the state-of-the-art top-k HUIM algorithms of other category.
Table 22. An overview of other top-k HUIM algorithms
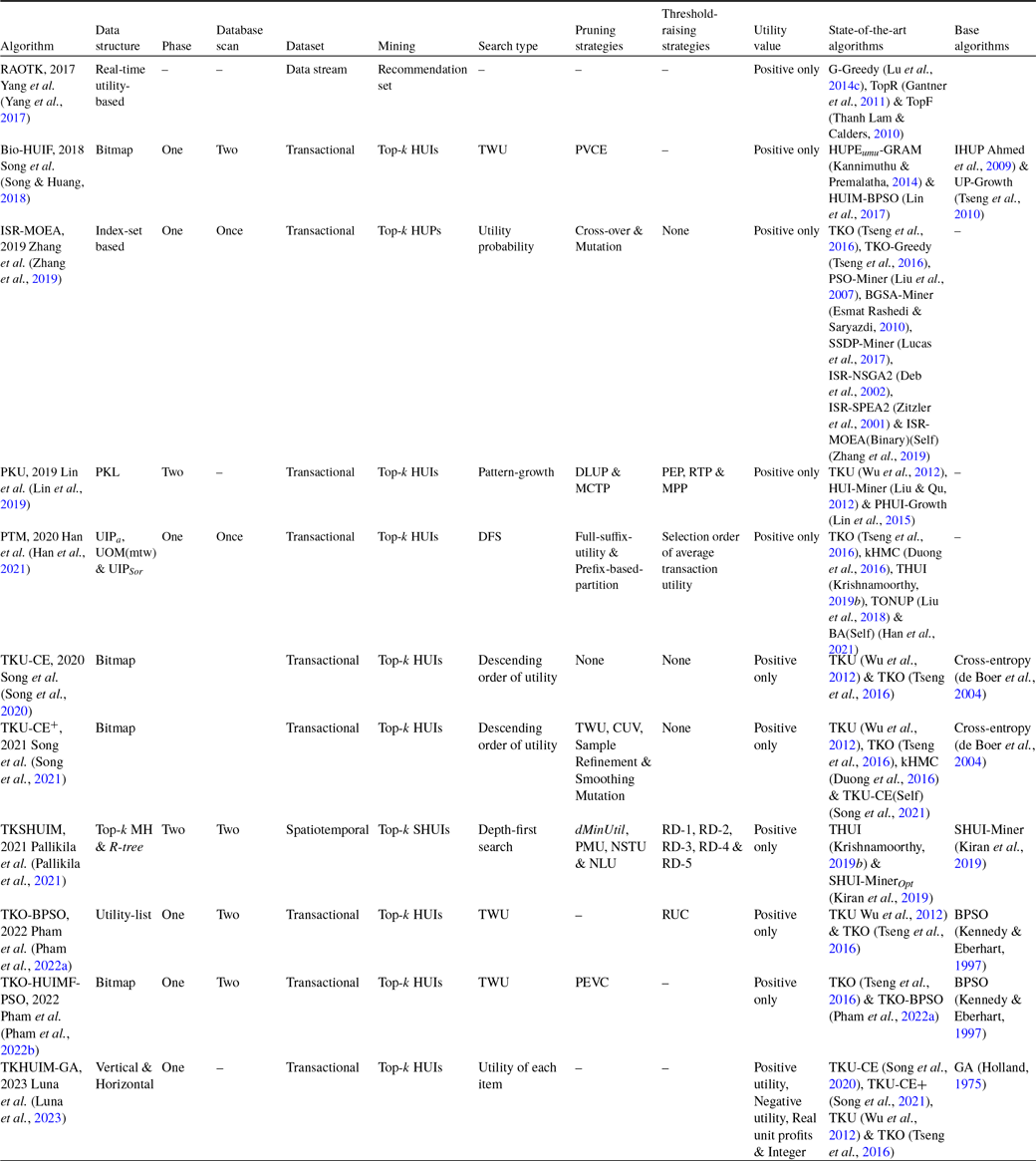
Table 23. Advantages and disadvantages of other top-k HUIM algorithms
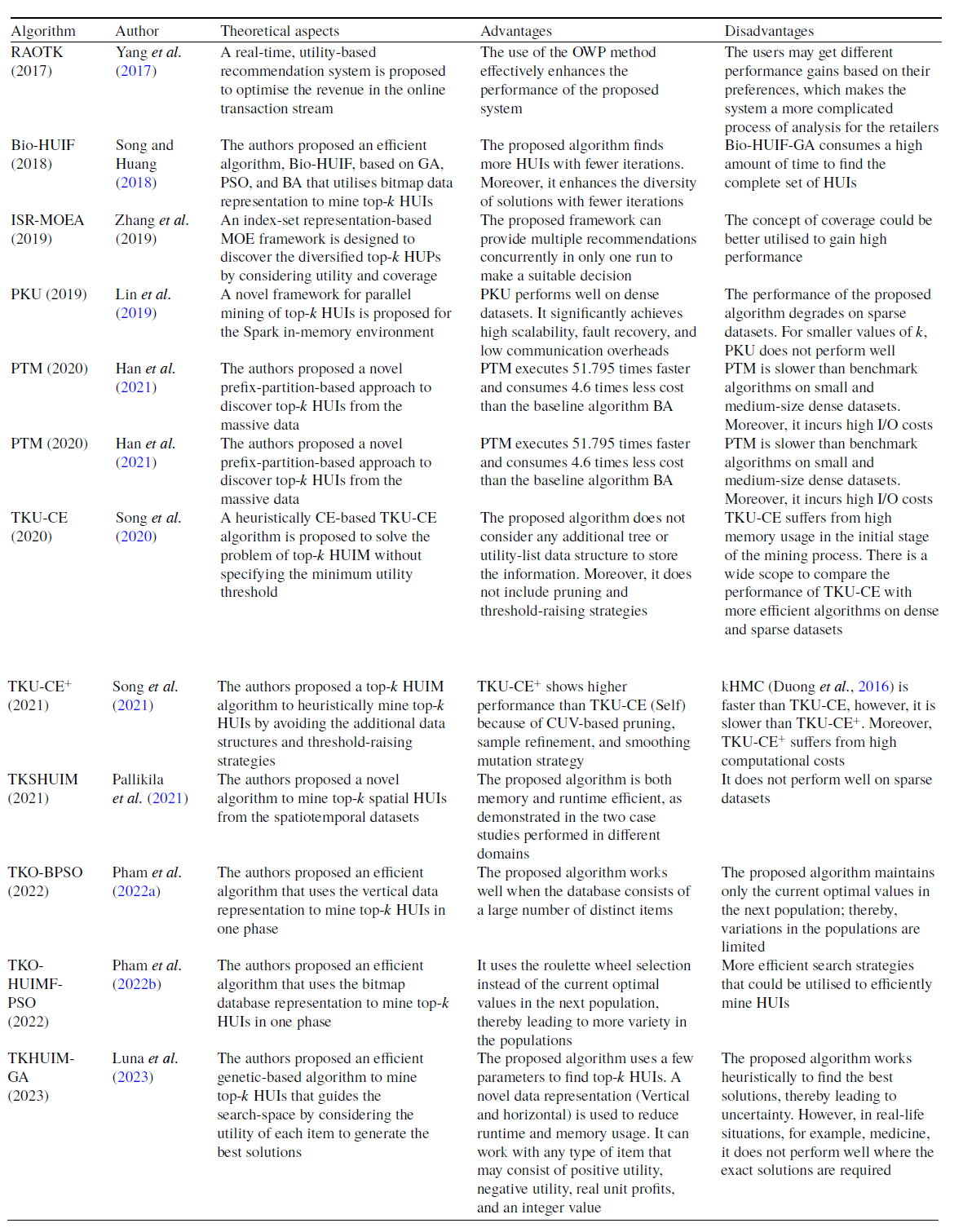
4. Discussions and summary
In this survey paper, we have discussed the top-k HUIM algorithms in-depth that are mainly divided into two categories: tree-based and utility-list-based. The tree-based top-k HUIM algorithms are further classified based on the utilized datasets: static, incremental, data stream, and sequential datasets. The utility-list-based top-k HUIM algorithms are further categorized into basic utility-list and extended utility-list. We have also discussed the top-k algorithms that consider both positive and negative utility profit. The main objectives of these algorithms are to design efficient upper bounds, data structures, pruning strategies, and threshold-raising strategies that, respectively, reduce the unpromising candidates, provide efficient memory usage, prune the search-space, and quickly raise the internal threshold.
Tree-based top-k HUIM algorithms, TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012) and REPT (Ryang & Yun, Reference Ryang and Yun2015), adopt a two-phase approach to find top-k HUIs. They suffer from multiple dataset scans and numerous unpromising candidates. Moreover, they do not work for large values of k. To deal with these issues, one-phase tree-based algorithms, TKEH (Singh et al., Reference Singh, Singh, Kumar and Biswas2019b) and TONUP (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018), are proposed to mine top-k HUPs. However, TKEH does not perform well on highly sparse datasets. TONUP is a memory-resident-based algorithm; hence, it may lead to scalability issues. Moreover, these algorithms are applicable only for positive utility. Therefore, TOPIC (Chen et al., Reference Chen, Wan, Gan, Chen and Fujita2021) is proposed to find top-k HUIs with both positive and negative utility. The vertical list-based one-phase algorithms TKO (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016), kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), and TKUL-Miner (Lee & Park, Reference Lee and Park2016) are designed to efficiently find the top-k HUIs from the transactional datasets. However, they work for positive utility only. Moreover, they mine top-k HUIs across the same time periods, which is not beneficial for business-makers. To deal with these issues, another list-based KOSHU algorithm (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) is proposed to mine top-k on-shelf HUIs with both positive and negative utility. However, it does not work well for longer periods of time. Another list-based one-phase THUI algorithm (Krishnamoorthy, Reference Krishnamoorthy2019 b) is proposed to efficiently mine top-k HUIs from the transactional dataset. However, it only works for small and/or medium-sized data that can be entirely stored in memory. The average utility plays a vital role in real-time applications. Therefore, an efficient one-phase TKAU algorithm (Wu & He, Reference Wu and He2018) is designed to find top-k HAUIs from the transactional dataset. However, these algorithms (Krishnamoorthy, Reference Krishnamoorthy2019b; Wu & He, Reference Wu and He2018) work only for positive unit profits. To deal with this issue, the TopHUI algorithm (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) is proposed to mine top-k HUIs from the transactional dataset with both positive and negative unit profits. However, it suffers from the same drawbacks as FHN (Fournier-Viger, Reference Fournier-Viger, Luo, Yu and Li2014).
The previous tree-based and utility-based top-k HUIM algorithms only work for static datasets. They are not applicable to incremental, data stream, or sequential datasets. To address these issues, a two-phase pattern-growth T-HUDS algorithm (Zihayat & An, Reference Zihayat and An2014) is developed to find top-k HUIs from a data stream. However, it has the same drawbacks as the two-phase methods. To deal with these issues, another pattern-growth TOPK-SW algorithm (Lu et al., Reference Lu, Liu and Wang2014a) is designed to find top-k HUIs over the sliding windows from a data stream. However, it does not work efficiently on sparse datasets. A vertical utility-list-based one-phase algorithm, Vert_top-k_DS (Dawar et al., Reference Dawar, Sharma and Goyal2017), is proposed to efficiently mine top-k HUIs over each sliding window from a data stream. However, it has a large number of intersections of inverted-list (iList), thereby resulting in the degradation of mining performance.
In the last decade, HUSPM has become the core emerging area of data mining among researchers. Therefore, the TUS algorithm (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013) is designed to find top-k HUSPs from the sequential dataset. However, it takes a lot of time to prune the unpromising candidates. Moreover, a few top-k HUSPs may be missed in the mining process. Utility episode mining is another important area of data mining. The TUP algorithm (Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016) is designed to mine top-k HUEs from the sequential dataset. However, it does not work properly on sparse datasets. Three efficient algorithms, TKHUS-Span
![]() $_{GDFS}$
(Wang et al., Reference Wang, Huang and Chen2016), TKHUS-Span
$_{GDFS}$
(Wang et al., Reference Wang, Huang and Chen2016), TKHUS-Span
![]() $_{BFS}$
(Wang et al., Reference Wang, Huang and Chen2016), and TKHUS-Span
$_{BFS}$
(Wang et al., Reference Wang, Huang and Chen2016), and TKHUS-Span
![]() $_{Hybrid}$
(Wang et al., Reference Wang, Huang and Chen2016), are proposed to mine top-k HUSPs from the sequential dataset by using GDFS, BFS, and hybrid of DFS and BFS, respectively. However, TKHUS-Span
$_{Hybrid}$
(Wang et al., Reference Wang, Huang and Chen2016), are proposed to mine top-k HUSPs from the sequential dataset by using GDFS, BFS, and hybrid of DFS and BFS, respectively. However, TKHUS-Span
![]() $_{GDFS}$
consumes lots of time to traverse the nodes. TKHUS-Span
$_{GDFS}$
consumes lots of time to traverse the nodes. TKHUS-Span
![]() $_{BFS}$
consumes a high amount of memory. The previous algorithms (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013; Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016;Wang et al., Reference Wang, Huang and Chen2016) work only in cases of positive utility. To address this issue, the Topk-NSP
$_{BFS}$
consumes a high amount of memory. The previous algorithms (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013; Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016;Wang et al., Reference Wang, Huang and Chen2016) work only in cases of positive utility. To address this issue, the Topk-NSP
![]() $^+$
algorithm (Dong et al., Reference Dong, Qiu, Lü, Cao and Xu2019) is designed to mine top-k NSPs from the sequential dataset. Another efficient TKUS algorithm (Zhang et al., Reference Zhang, Du, Gan and Yu2021) is proposed to find top-k HUSPs from the sequential dataset. It ensures that no top-k HUSPs are missed in the mining process. THUE (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021) is proposed to discover all top-k HUEs from the sequential dataset. Although these previous algorithms efficiently mined top-k HUSPs. However, there is wide scope to design efficient pruning strategies and threshold-raising strategies to improve mining performance.
$^+$
algorithm (Dong et al., Reference Dong, Qiu, Lü, Cao and Xu2019) is designed to mine top-k NSPs from the sequential dataset. Another efficient TKUS algorithm (Zhang et al., Reference Zhang, Du, Gan and Yu2021) is proposed to find top-k HUSPs from the sequential dataset. It ensures that no top-k HUSPs are missed in the mining process. THUE (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021) is proposed to discover all top-k HUEs from the sequential dataset. Although these previous algorithms efficiently mined top-k HUSPs. However, there is wide scope to design efficient pruning strategies and threshold-raising strategies to improve mining performance.
The various lower-bounds, upper-bounds, and data structures used by the top-k HUIM algorithms are discussed. The PEM structure is used to store the lower bounds of the utilities of 2-itemsets (Wu et al., Reference Wu, Shie, Tseng and Yu2012). The PUM structure (Ryang & Yun, Reference Ryang and Yun2015) is used for the PIU threshold-raising strategy, and it calculates the lower-bound utilities of 2-itemsets. The RSD matrix is used for RSD strategy and computes the utilities of their possible 2-itemsets (Ryang & Yun, Reference Ryang and Yun2015). The ECUS structure is implemented by using hash-map and stores only those values for that TWU not equal to 0. The CUDM structure is used to store the utilities of pairs of items. Then, the COVL structure is utilized to store values from CUDM during the COV strategy (Singh et al., Reference Singh, Singh, Kumar and Biswas2019b). The iCAUL (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018) is a memory-resident data structure, an improved version of CAUL (Liu et al., Reference Liu, Wang and Fung2012), that computes the utilities of enumerated patterns. An array-based UC technique (Chen et al., Reference Chen, Wan, Gan, Chen and Fujita2021) is used to calculate the TWU and upper bound of itemsets in linear time. The RLU upper-bound (Chen et al., Reference Chen, Wan, Gan, Chen and Fujita2021), adopted from the EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015), consists of both positive and negative utility. It is tighter than TWU. RSU upper-bound (Chen et al., Reference Chen, Wan, Gan, Chen and Fujita2021), which also adopts from EFIM (Zida et al., Reference Zida, Fournier-Viger, Lin, Wu and Tseng2015), efficiently prunes the search-space. It is tighter than Remaining Utility (RU) (Liu & Qu, Reference Liu and Qu2012). The EUCST structure (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), an extension of EUCS (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014), is performed during the second dataset scan. It avoids the costly join operations and occupies less memory to efficiently mine the top-k HUIs. The TEP upper bound (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) greatly reduced the number of extensions to be explored to mine HUIs. The EMPPS structure (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) is implemented using a triangular matrix. It reorders the items according to the increasing order of RTWU values in such a way that all negative items succeed the positive items. The HUI-tree structure (Lu et al., Reference Lu, Liu and Wang2014a) keeps the utilities of itemsets according to the lexicographical order corresponding to the current window. A fixed-size sorted TUSList structure (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013) is used to keep the top-k HUSPs dynamically, and the minimum-utility threshold is set to prune the unpromising candidates. The SWU upper bound (Wang et al., Reference Wang, Huang and Chen2016) calculates the utilities of sequences and their sub-sequences and the actual utility of candidates. But it generates excessive candidates. To solve this problem, two tighter upper bounds, PEU and RSU (Wang et al., Reference Wang, Huang and Chen2016), are proposed. Two tighter upper bounds, SPU (Zhang et al., Reference Zhang, Du, Gan and Yu2021) and SEU (Zhang et al., Reference Zhang, Du, Gan and Yu2021), are proposed to effectively prune the search-space by using the DCP, thereby resulting in the improvement of the mining process. An inverted-list, iList data structure (Dawar et al., Reference Dawar, Sharma and Goyal2017), an adaptation of utility-list (Liu & Qu, Reference Liu and Qu2012), and a FIFO queue maintain the utility information of the itemsets across sliding windows by scanning the dataset twice according to the increasing order of TWU. It performs both insertion and deletion very rapidly. The LIU structure (Krishnamoorthy, Reference Krishnamoorthy2019 b) is a triangular matrix that maintains the utility information of the contiguous itemset concisely. A utility lower bound, LIU-LB (Krishnamoorthy, Reference Krishnamoorthy2019 b), significantly increases the minimum-utility threshold without the need to compute the actual utility of the long itemsets. The AUO-List structure (Wu & He, Reference Wu and He2018) maintains the utility information of itemsets and facilitates the pruning strategies, EMUP, and EA in a compact form. But it needs to perform excessively costly join operations. A vertical list-based PNU-list structure (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020), adopted from FHN (Fournier-Viger, Reference Fournier-Viger, Luo, Yu and Li2014), computes the total utility, remaining utility (RU), total positive utility, and total negative utility of the intended itemsets from the dataset.
In this survey paper, we have discussed the various pruning strategies of top-k HUIM algorithms. The DGU pruning strategy is used to eliminate the unpromising itemsets and their utilities from the transaction during the first scan (Ryang & Yun, Reference Ryang and Yun2015). The DGN strategy is used to decrease the utilities of nodes during tree construction according to their decreasing order (Ryang & Yun, Reference Ryang and Yun2015). The DLU strategy eliminates the local unpromising itemsets and their estimated utilities in the tree (Ryang & Yun, Reference Ryang and Yun2015). The DLN strategy is used to construct the local tree, also called a conditional pattern tree, during tree construction (Ryang & Yun, Reference Ryang and Yun2015). The pruning strategies EUCP (based on EUCS structure) and SUP are used to efficiently prune the search-space (Singh et al., Reference Singh, Singh, Kumar and Biswas2019b). The EUCPT strategy (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), an improved version of EUCP (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014), utilizes the item co-occurrences information to reduce the search-space by utilizing the EUCST structure. The EA strategy (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) is used to obtain good performance for the utility-list construction in the mining process. However, it can be applied only when the utility list is completely constructed. The EMPRP strategy (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) computes the utilities of each 1-itemset and all 2-itemsets by using the EMPRS structure. It avoids the costly join operations. However, some pairs of items may not appear simultaneously in any transaction. To deal with this issue, the CE2P strategy (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) is proposed by using the bit matrix. It avoids the large number of utility-list join operations. This strategy is effective on sparse and very large datasets. Another pruning strategy, PUP (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017), is proposed to further reduce the utility-list join operations. The SRU strategy (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013) is used to keep refreshing the blacklist until all the itemsets in the whitelist ensure that the SRU of an itemset is no less than the minimum-utility threshold. The EWU strategy (Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016) is used to explore those itemsets first that have higher EWU values as compared to others. However, it works better on dense datasets. A utility-chain structure (Wang et al., Reference Wang, Huang and Chen2016) is proposed to efficiently calculate the values of PEU, RSU, and utility of the itemsets. The TDE strategy (Zhang et al., Reference Zhang, Du, Gan and Yu2021) limits the number of dataset scans. It reduces the unpromising candidates in the LQS-tree by using the depth-first method. A width-based EUI strategy (Zhang et al., Reference Zhang, Du, Gan and Yu2021) stops the new branches in LQS-tree. It ensures the acquisition of the complete set of top-k HUIs. The optimized EWU
![]() $_{opt}$
strategy (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021), optimized version of EWU (Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016), is proposed to traverse the tree using the depth-first method. The EMUP strategy (Wu & He, Reference Wu and He2018) greatly reduces the large number of costly join operations performed by AUO-List. The RTWU-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) prunes the candidates by using the depth-first method if the RTWU value of the candidate is no less than the minimum utility threshold. The RU-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) states that if the sum of positive utility and remaining utility of an itemset is no more than the minimum threshold, then that itemset is not top-k HUI and hence can be eliminated from the mining process. The LA-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) states that if the sum of overall utility and remaining utility of an itemset is no more than the minimum threshold, then this itemset is discarded. The L-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) states that if the utility of the leaf node is no more than the minimum threshold, then there is no need to evaluate the extension of those itemsets.
$_{opt}$
strategy (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021), optimized version of EWU (Rathore et al., Reference Rathore, Dawar, Goyal, Patel, Deshpande, Ravindran and Ranu2016), is proposed to traverse the tree using the depth-first method. The EMUP strategy (Wu & He, Reference Wu and He2018) greatly reduces the large number of costly join operations performed by AUO-List. The RTWU-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) prunes the candidates by using the depth-first method if the RTWU value of the candidate is no less than the minimum utility threshold. The RU-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) states that if the sum of positive utility and remaining utility of an itemset is no more than the minimum threshold, then that itemset is not top-k HUI and hence can be eliminated from the mining process. The LA-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) states that if the sum of overall utility and remaining utility of an itemset is no more than the minimum threshold, then this itemset is discarded. The L-prune strategy (Gan et al., Reference Gan, Wan, Chen, Chen and Qiu2020) states that if the utility of the leaf node is no more than the minimum threshold, then there is no need to evaluate the extension of those itemsets.
A brief discussion about the various threshold-raising strategies of top-k HUIM algorithms is elaborated. To mine the new Potential top-K HUIs (PKHUIs), the MC threshold-raising strategy determines that if its Minimum Item Utility (MIU), TWU, and Maximum Utility (MAU) are no less than the current border minimum-utility threshold, then it is safe to use the MIU of an itemset to raise the border threshold (Wu et al., Reference Wu, Shie, Tseng and Yu2012). The PE is used to raise the border threshold during the first dataset scan (Wu et al., Reference Wu, Shie, Tseng and Yu2012). The NU is performed during the construction of UP-Tree (Wu et al., Reference Wu, Shie, Tseng and Yu2012). The MD is performed after the UP-Tree construction and before the PKHUIs generations (Wu et al., Reference Wu, Shie, Tseng and Yu2012). It takes a lot of time to check the large number of PKHUIs in the dataset. To deal with this issue, SE is performed to sort the candidates in the decreasing order of estimated utilities during the second phase (Wu et al., Reference Wu, Shie, Tseng and Yu2012). The PIU strategy (Ryang & Yun, Reference Ryang and Yun2015) is performed to increase the current minimum-utility threshold set to 0 during the first scan. The RIU strategy (Ryang & Yun, Reference Ryang and Yun2015) discards those unpromising itemsets that have smaller TWUs than the raised threshold and selects N promising itemsets. The RSD and NU strategies are further used to raise the threshold (Ryang & Yun, Reference Ryang and Yun2015). The EUCST strategy, proposed by FHM (Fournier-Viger et al., Reference Fournier-Viger, Wu, Zida and Tseng2014) and improved by kHMC (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016), effectively raises the minimum-utility threshold and prunes the search-space. The CUD and COV strategies (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) raise the threshold using the 2-itemsets stored in the EUCS structure. The CUD is performed after the RIU strategy. iCAUL maintains the autoMaterial strategy (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018) to balance the pseudo-projection and materialized projection of the transaction set by using the self-adjusting threshold. The reason is that pseudo-projection works well on sparse datasets, while materialized projection is good on dense datasets. The DynaDescend strategy (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018) effectively raises the border threshold and prunes search-space by dynamically resorting the items according to the decreasing order of local utility upper-bound. However, it incurs additional costs. The ExactBoarder strategy (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018) is used to rapidly raise the border threshold by using the exact utility of each enumerated pattern. The SuffixTree strategy (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018) effectively maintains the shortlisted patterns by using the suffix tree. The OppoShift strategy (Liu et al., Reference Liu, Zhang, Fung, Li and Iqbal2018) is used to opportunistically shift to a two-round approach when the enumerated patterns are very long. However, it is computationally expensive. The RUZ strategy (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) is performed during the candidate generations to search the top-k HUIs, while the EPB strategy (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) is performed to generate the candidates that have the highest utility first. Two threshold-raising strategies, RIRU and RIRU2, are proposed to quickly raise the threshold during the first and second dataset scans of the mining process (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017). The FCU strategy (Lee & Park, Reference Lee and Park2016) is performed from the first child node in the tree. The advantage is that the first child node does not affect the other nodes. Therefore, it generates all the promising candidates. The FSD strategy searches 1-itemsets according to the descending order of TWU values in the TKUL-Miner algorithm (Lee & Park, Reference Lee and Park2016). It quickly raises the border threshold and efficiently prunes the search-space. The maxUtilList (Zihayat & An, Reference Zihayat and An2014; Dawar et al., Reference Dawar, Sharma and Goyal2017) of a HUDS-tree initializes the threshold during the construction and update of the HUDS-tree. The MIUList (Zihayat & An, Reference Zihayat and An2014; Dawar et al., Reference Dawar, Sharma and Goyal2017) dynamically adjusts the threshold by maintaining the top-k MIU values of current promising HUIs. The minTopKUtil (Zihayat & An, Reference Zihayat and An2014; Dawar et al., Reference Dawar, Sharma and Goyal2017) adjusts the threshold by using the utilities of top-k HUIs in the last sliding window and is performed during the second phase of the mining process. The Pre-insertion and sort concatenation strategies (Yin et al., Reference Yin, Zheng, Cao, Song and Wei2013) effectively raise the threshold in the TUSList structure. SRU quickly raises the minimum-utility threshold as fast as possible and ensures that no top-k HUIs miss from the mining process. The RTU strategy (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021) utilizes the hash-map structure to calculate each simultaneous event set. The RUC strategy (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021) uses the priority queue structure to keep the top-k HUEs according to the descending order of utilities of episodes. The LIU-E strategy (Krishnamoorthy, Reference Krishnamoorthy2019 b) effectively raises the threshold during the initial stages of the mining process. The EPBF (Wu & He, Reference Wu and He2018) is performed after the initial construction of the AUO-List of 1-itemsets. It extends the itemsets that have a large average utility first because these itemsets may have a high probability of having a high average utility.
5. Future directions
Top-k HUIM has many applications. However, it has some fundamental limitations. To address these issues, extensions of the problem of top-k HUIM can be proposed. This section aims at providing future directions by extending these algorithms. One of the limitations of the top-k HUIM problem is that a lot of smaller itemsets may be found by the algorithms, which often need to be generated first. Finding too many smaller itemsets is an issue because users typically do not have much time to analyze a large amount of itemsets with these smaller itemsets. Moreover, as more itemsets are found, the performance of algorithms decreases in terms of memory and runtime. To address this issue, a solution is to discover concise representations of top-k HUIs instead of all top-k HUIs. There are two main concise representations of top-k HUIM, for example, closed and constraint-based.
5.1 Closed top-k HUIs
Closed HUIs are the itemsets that do not have super-sets having the same support count. The discovery of closed top-k HUIs instead of all top-k HUIs reduces the number of itemsets. Hence, closed top-k HUIs are more interesting and actionable because they are a lossless representation of all the top-k HUIs. In other words, using closed top-k HUIs, the information about all top-k HUIs, including their support, can be recovered without scanning the dataset. Closed itemsets are more actionable because they represent the largest set of all top-k HUIs. Recently, many closed algorithms for HUIs have been proposed (Wu et al., Reference Wu, Fournier-Viger, Gu and Tseng2015; Fournier-Viger et al., Reference Fournier-Viger, Zida, Lin, Wu and Tseng2016). But till now, no algorithm has been presented for closed top-k HUIs. Therefore, closed top-k HUIs are a good area to explore. The coverage concept of the kHMC algorithm (Duong et al., Reference Duong, Liao, Fournier-Viger and Dam2016) could be further explored to significantly prune the search-space in other HUIM algorithms, for example, closed and maximal HUIM. Similarly, the KOSHU algorithm (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) could be further developed for closed and maximal on-shelf HUIM. A detailed survey of closed HUIM algorithms is available in Singh et al. (Reference Singh, Singh, Luhach, Kumar and Biswas2021).
5.2 Constraint-based top-k HUIs
Although a top-k HUIM uncovers thousands of high-utility itemsets, the end user is particularly interested in only long and more actionable itemsets. Efficient mining for only the itemsets that satisfy user-specified constraints is called constraint-based mining. To fulfil the end-user requirements, length-based HUIM (Fournier-Viger et al., Reference Fournier-Viger, Lin, Duong and Dam2016a; Singh & Biswas, Reference Singh and Biswas2019) plays an important role. Two upper bounds (minimum length and maximum length) can be defined to mine length-based top-k HUIs. To remove the tiny items, the user can set the minimum length threshold with k. Length-based top-k HUIs can remove lots of small itemsets and produce more interesting and actionable HUIs. A maximum length constraint can be applied to prune too large itemsets (Singh et al., Reference Singh, Kumar, Singh, Shakya and Biswas2019a). Therefore, minimum and maximum length based constraint can be utilized with top-k HUIM algorithms. To find rules more efficiently, we need to push the constraint as deep as we can. In other words, the constraints are applied during the search for itemsets to reduce the search-space. The algorithms adopting this approach can be orders of magnitude faster and generate much fewer itemsets than top-k HUIM algorithms, depending on the utilized constraints.
5.3 Negative utility based top-k HUIM
Top-k HUIM focuses on the discovery of items that are positively correlated in the dataset. However, for some applications, negative utility mining is more interesting than positive utility mining. A negative utility itemset contains the negation of at least one item. Mining negative HUIs is more difficult than mining only positive HUIs as the search-space becomes larger. Initially, to mine negative HUIs, the HUINIV (Chu et al., Reference Chu, Tseng and Liang2009) algorithm was proposed. A detailed survey of negative utility based HUIM approaches is presented by Singh et al. (Reference Singh, Singh, Kumar and Biswasn.d.). But none of the algorithms are available for mining top-k HUIs with negative utility. Hence, in the future, this problem can also be explored. The TKN (Ashraf et al., Reference Ashraf, Abdelkader, Rady and Gharib2022) algorithm can be further extended on the different top-k mining variations that include top-k local and peak HUIM, periodic HUIM, and closed HUIM. Topk-NSP
![]() $^+$
(Dong et al., Reference Dong, Qiu, Lü, Cao and Xu2019) considers the influence of PSPs on NSPs mining; however, more effective methods could be further designed to mine useful NSPs. It is an open issue to find the correctness and completeness of the Topk-NSP
$^+$
(Dong et al., Reference Dong, Qiu, Lü, Cao and Xu2019) considers the influence of PSPs on NSPs mining; however, more effective methods could be further designed to mine useful NSPs. It is an open issue to find the correctness and completeness of the Topk-NSP
![]() $^+$
algorithm to find the intended patterns.
$^+$
algorithm to find the intended patterns.
5.4 Top-k HUIM from data stream
Another limitation of top-k HUIM algorithms is that the datasets are assumed to be static. Top-k HUIM algorithms are said to be batch algorithms, as they are designed to be applied once to a dataset to obtain rules. Then, if the dataset is updated, algorithms need to be run again to obtain the updated rules. This type of approach is not efficient because sometimes only small changes are made to the datasets, and algorithms have to scan the whole dataset again to mine rules. A solution to this problem is to design a top-k HUIM algorithm with dynamic datasets. To the best of our knowledge, T-HUDS (Zihayat & An, Reference Zihayat and An2014) is the only promising algorithm to mine top-k HUIs from a data stream. T-HUDS is a two-phase algorithm; hence, there is wide scope to implement efficient one-phase algorithms. Similar to tree structures used in HUPMS (Ahmed et al., Reference Ahmed, Tanbeer, Jeong and Choi2012) and TKU (Wu et al., Reference Wu, Shie, Tseng and Yu2012), T-HUDS utilizes an HUDS-tree structure that is lossy compression of the transaction in a sliding window. The sliding window is small enough to fit entirely in memory. It can greatly reduce the scans to enhance the mining performance. However, a lossless compression structure can be further designed to keep the information needed to calculate the exact utility. The approximation methods can also be further developed to generate an approximate list of top-k patterns from the lossy compressed information. The Vert
![]() $\_$
top-k_DS algorithm (Dawar et al., Reference Dawar, Sharma and Goyal2017) could be further developed in other data stream models.
$\_$
top-k_DS algorithm (Dawar et al., Reference Dawar, Sharma and Goyal2017) could be further developed in other data stream models.
5.5 Top-k HUIM in Big data environment
The TKUS (Zhang et al., Reference Zhang, Du, Gan and Yu2021) algorithm could be further applied in the big data environment. The different extensions of TKUS could be considered; for example, Hadoop is used to enhance the mining speed of the algorithm. It would be interesting to design a parallel and distributed version of the KOSHU algorithm (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) that could be run on massive data. The REPTPLUS algorithm (Le et al., Reference Le, Truong and Tran2017) could be further developed to effectively address the issues of large and distributed datasets in parallel model environments. There is wide scope to develop the distributed version of TKQ (Nouioua et al., Reference Nouioua, Fournier-Viger, Gan, Wu, Lin, Nouioua, Li, Yue, Jiang, Chen, Li, Long, Fang and Yu2022) in big data environments. The Vert
![]() $\_$
top-k_DS algorithm (Dawar et al., Reference Dawar, Sharma and Goyal2017) has enough room to apply to big data, for example, Apache Strom and Apache Spark. Another interesting research opportunity is to redesign the TKAU algorithm (Wu & He, Reference Wu and He2018) as a distributed algorithm to find the top-k HAUIs in the big data.
$\_$
top-k_DS algorithm (Dawar et al., Reference Dawar, Sharma and Goyal2017) has enough room to apply to big data, for example, Apache Strom and Apache Spark. Another interesting research opportunity is to redesign the TKAU algorithm (Wu & He, Reference Wu and He2018) as a distributed algorithm to find the top-k HAUIs in the big data.
5.6 Other top-k HUIM problems
Some other extensions of top-k HUIs that can mine rich itemsets in various ways, such as mining itemsets from uncertain data, Fuzzy top-k HUIM, top-k high utility sequential itemset mining, periodic top-k HUIM, episode top-k HUIM, and top-k on-shelf HUIM, etc. The THUE (Wan et al., Reference Wan, Chen, Gan, Chen and Goyal2021) algorithm could be further developed to find different types of episodes, for example, parallel and closed episodes. Moreover, the useful minimum utility based strategies could be further designed to improve mining performance. The design of the distributed version of THUE is an interesting and challenging opportunity for researchers. There is a wide room for the further exploration of the TKO algorithm (Tseng et al., Reference Tseng, Wu, Fournier-Viger and Yu2016) in the area of top-k HUE, top-k closed
![]() $^+$
HUI, top-k high utility web access patterns, and top-k mobile HUSPs. There is an interesting research direction to design the approximate version of the KOSHU algorithm (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) that would return the approximate list of top-k on-shelf HUIM. The mining performance of the THUI algorithm (Krishnamoorthy, Reference Krishnamoorthy2019
b) could be further improved by materializing more promising non-contiguous itemsets. Another open research opportunity is to adopt the THUI algorithm for the other top-k HUIM variants, for example, on-shelf HUIM, data stream mining, and sequential pattern mining. Another interesting future work is to mine HAUIs and strongly associated itemsets (Wu & He, Reference Wu and He2018) with combined criteria. There is ample research opportunity to redesign the TKC algorithm (Nouioua et al., Reference Nouioua, Wang, Fournier-Viger, Lin and Wu2020) in the other top-k HUIM variants, high average utility patterns (Singh et al., Reference Singh, Kumar and Biswas2022) and soft computing (Kumar & Singh, Reference Kumar and Singh2022).
$^+$
HUI, top-k high utility web access patterns, and top-k mobile HUSPs. There is an interesting research direction to design the approximate version of the KOSHU algorithm (Dam et al., Reference Dam, Li, Fournier-Viger and Duong2017) that would return the approximate list of top-k on-shelf HUIM. The mining performance of the THUI algorithm (Krishnamoorthy, Reference Krishnamoorthy2019
b) could be further improved by materializing more promising non-contiguous itemsets. Another open research opportunity is to adopt the THUI algorithm for the other top-k HUIM variants, for example, on-shelf HUIM, data stream mining, and sequential pattern mining. Another interesting future work is to mine HAUIs and strongly associated itemsets (Wu & He, Reference Wu and He2018) with combined criteria. There is ample research opportunity to redesign the TKC algorithm (Nouioua et al., Reference Nouioua, Wang, Fournier-Viger, Lin and Wu2020) in the other top-k HUIM variants, high average utility patterns (Singh et al., Reference Singh, Kumar and Biswas2022) and soft computing (Kumar & Singh, Reference Kumar and Singh2022).
6. Conclusion
In this paper, we have presented a detailed survey of top-k HUIM approaches. We also discussed the important preliminary definitions of the HUIM and top-k HUIM problems. The paper presented three broad categories of top-k HUIM algorithms: tree-based, utility-list-based, and other hybrids. The paper showed a comparative analysis of the available state-of-the-art top-k HUIM approaches for each category. This survey also discussed the comparative advantages and disadvantages of each category. The paper also presented important future directions for top-k HUIM problems that address some shortcomings of top-k HUIM. In addition, the paper discussed other research problems and research opportunities related to top-k HUIM, such as concise top-k HUIM, constraint-based top-k HUIM, negative utility-based top-k HUIM, and top-k HUIM from the data stream. In the future, we can extend this work with an experimental comparison.
Funding
No funding has been received for this work.
Competing interests
The authors declare no conflicts of interest. This article does not contain any studies with human participants or animals performed by any of the authors. The article presents a review of top-k high-utility itemset mining approaches.
Authors contribution statement
Author Contributions K.S. conceived the analysis idea and presented the taxonomy. R.K. developed the theory and analysis of the state-of-the-art approaches. R.K. provided the data for Tables 6–23. K.S. implemented the example and tables related to the running example. R.K. performed the analysis part at Section 3. K.S. collected all the required data. K.S. reviewed and edited the manuscript. Both the authors analyzed and contributed to the final manuscript.
Data availability and access
Our work does not have any data to explore. Data sharing is not applicable to this article, as no datasets were generated or analyzed during the current study.