1 Introduction
Students believe that they are especially likely to be called on to answer a question in class if they have not done the required reading (Reference Risen and GilovichRisen & Gilovich, 2008), and people believe that they are especially likely to experience a mishap while traveling if they have not purchased travel insurance (Reference TykocinskiTykocinski, 2008). Both are instances of magical thinking where people who “tempt fate” by not taking necessary precautions feel that they are more likely to suffer negative consequences. Conversely, reminding people of precautions they have taken—for example, having purchased health insurance—leads them to see related risks as less likely (Reference TykocinskiTykocinski, 2008), a phenomenon we refer to as the “protection effect”. In the present research we examined both the tempting fate effect and the protection effect. We found consistent support for the tempting fate effect, but no support for the protection effect.
1.1 Tempting fate
When people tempt fate by neglecting to protect themselves from possible negative outcomes, they feel that those very negative outcomes are, ironically, more likely to occur. Reference Risen and GilovichRisen and Gilovich (2008) detail how and why exactly the tempting fate effect occurs. Briefly, they argue that the act of tempting fate heightens the accessibility of negative outcomes. This heightened accessibility then leads to higher perceived probabilities of those outcomes (via the availability heuristic; Reference Tversky and KahnemanTversky & Kahneman, 1974). Reference Tversky and KahnemanTykocinski (2008) investigated how tempting fate beliefs affected the risk judgments of people who imagined having or not having insurance, and found that those who imagined that they were unable to purchase travel insurance believed that they were consequently at greater risk of losing luggage or needing medical care during their travels. Tykocinski interpreted this result as consistent with a belief in tempting fate: Failing to protect oneself by purchasing insurance brings negative outcomes to mind, which in turn makes those outcomes seem more likely.
1.2 Protection effect
In the research described above, Reference Tversky and KahnemanTykocinski (2008) also tested whether reminding people of precautions they have taken leads them to see associated risks as less likely. Specifically, she reminded people of their health insurance either before or after they rated the probability of needing medical care in the near future. Indeed, people who were reminded of their insurance before answering these questions thought they were less likely to need medical care than those who were reminded afterwards—the “protection effect”. Tykocinski argued that this effect occurs because reminding people of precautions primes a general mindset of safety, making risks seem less likely.
1.3 The current research
While tempting fate and the protection effect might seem to be different sides of the same coin, there is reason to expect that the two effects might not be equally strong. Across many domains of judgment, “bad is stronger than good”—that is, negative information has stronger effects on judgment than does positive information (Reference Baumeister, Bratslavsky, Finkenauer and VohsBaumeister, Bratslavsky, Finkenauer, & Vohs, 2001). Consequently, one might expect tempting fate beliefs, which are motivated by the heightened accessibility of negative outcomes, to show more robust effects on judgment than the protection effect, which putatively results from a mindset of safety. Here, we report five studies in which we examine both phenomena. We begin by reporting a study—which was conducted as part of a larger project concerning people’s thinking about insurance—in which we closely replicated the Reference Tversky and KahnemanTykocinski (2008) protection effect study described above. As we were unable to replicate the protection effect, we ran 2 additional replications in which we tried to stay as close as possible to the original study. These also failed to uncover any evidence for a protection effect. Finally, we report two conceptual replications in which we simultaneously tested both the protection effect and tempting fate. Here, we found evidence for tempting fate, but again found no evidence of a protection effect.
In each of the studies we report confirmatory analyses, in which we replicate the analytical strategy reported in the original papers. In personal communication, Tykocinski suggested that the protection effect would be more likely to occur for older people. To test such post-hoc explanations of failures to replicate, we report possible moderators such as age and gender in exploratory analyses sections where possible. In addition, we report how we determined our sample size, all data exclusions (if any), all manipulations, and all measures in the study (following the recommendations of Reference Simmons, Nelson and SimonsohnSimmons, Nelson, & Simonsohn, 2012).
2 Study 1a: Reference Tversky and KahnemanTykocinski (2008) Exp. 1 with undergraduate subjects
This study aimed to replicate Experiment 1 reported in Reference Tversky and KahnemanTykocinski (2008). The hypothesis was that because, through commercials, insurance is associated with feelings of safety and protection, a reminder of insurance leads people to believe that they are less likely to be in need of medical care. We reproduced the procedure reported in Reference Tversky and KahnemanTykocinski (2008) as closely as possible, with the exception of the subject population. Whereas the original finding was based on data from train commuters in Israel, we ran the study in the Tilburg University social psychology lab and our subjects were Dutch undergraduate psychology students.
At the time we ran this study, we were not aware of the Reference Simmons, Nelson and SimonsohnSimmons, Nelson, and Simonsohn (2011) paper that details how running unreported conditions and measures can lead to higher false-positive rates. While running the present experiment we ran four other conditions and included one extra risk-taking measure. In the procedure we describe below we report only the conditions in which we replicate the method reported in Reference Tversky and KahnemanTykocinski (2008) and leave out measures that were recorded after the original method. Since we do not find significant differences between conditions, higher false-positive rates are less of a concern. Nevertheless, a table describing the complete experimental design and measures is available in the Appendix.
2.1 Method
Subjects. Thirty-five Tilburg University undergraduate psychology students participated in a 60-minute research session of unrelated experiments that ran for a week in September 2010. They were assigned to a reminded (n=18) or non-reminded (n=17) condition. Gender and age were not recorded, but usually this group consists of 70% females around the age of 20.
Materials and procedure. The insurance reminder required people to indicate the name of their health insurance plan and whether they had additional coverage. Subjects then rated the extent to which they were satisfied with their health insurance on a scale ranging from 1 = “not at all satisfied” to 7 = “very satisfied”.
The reminder was either preceded or followed by 7 questions that required people to rate the probability of different events happening within the next five years on a 5-point scale (1 = “very small chance”, 5 = “very big chance”). Specifically, they rated the probability that during the next 5 years they would have to undergo a serious operation, would require physiotherapy, or would need to stay in the hospital for a long time. The original third question mentioned “comprehensive nursing care” (Reference TykocinskiTykocinski, 2008, p. 1348) but we changed the wording to make the question more easily understandable for undergraduates. The remaining four items required subjects to rate the probability that they would lose a substantial amount of money, that a war would break out in Europe, that they would win the lottery, and that Israel and Palestine would sign a peace treaty.
2.2 Results
All subjects indicated that they had health insurance. (This is unsurprising, as health insurance is legally required in the Netherlands.) Fifteen (42.9%) indicated that they had some form of additional coverage. Mean satisfaction level was 5.17 (SD = 1.01) and there was no significant difference in satisfaction level between the reminded (M = 5.22, SD = 1.12) and non-reminded condition (M = 5.12, SD = 0.93), F(1, 33) = 0.09, p = .765, η2 = .003.
Confirmatory analysis. Mean evaluations of the probability of seven future events are shown in Table 1, along with univariate analyses of variance per item. The three health-related items were analyzed in a repeated-measures design with the reminder condition (reminded vs. non-reminded) as a between-subjects factor. Subjects who were reminded of their health insurance before they were asked about their likelihood of health problems did not differ in their ratings from those people who were reminded afterwards, F(1, 33) = 0.053, p = .819, η2 = .002. In addition, after Bonferonni corrections, there were no significant differences on the four remaining measures.
Table 1: Means, standard deviations, sample sizes, and test statistics for all probability ratings of future events in Study 1a per condition.
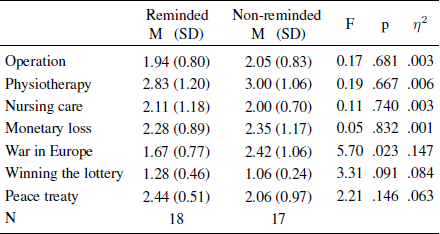
The central result is that we did not replicate Experiment 1 in Reference Tversky and KahnemanTykocinski (2008). In retrospect we determined that this study was underpowered; using G*Power (Reference Faul, Erdfelder, Lang and BuchnerFaul, Erdfelder, Lang, & Buchner, 2007) we found we had 76% power to find an effect as large as reported in the original study (η2 = .13, cohen’s f = 0.39). This might explain why we did not replicate the protection effect. In Study 1b, we ran a priori power calculations and determined that we needed at least 62 subjects to have 95% power to find an effect as large as reported in Reference Tversky and KahnemanTykocinski (2008).Footnote 1
Another possible reason for this initial failure to replicate the protection effect was that our subjects were undergraduates whereas Tykocinski’s subjects were commuters on a train. We were not in the position to fly to Israel to re-run the study with subjects from the original pool. We could, however, ask Dutch train commuters to fill out the survey. This is what we did in Study 1b.
3 Study 1b: Reference Tversky and KahnemanTykocinski (2008) Exp. 1 with train commuters
In the Netherlands, it is illegal to run studies in the train without a permit. Therefore, instead of in the train, commuters were asked to fill out the survey at or in front of the train station.
3.1 Method
Subjects. Seventy-eight commuters (M age= 32.55, range 16–74; 42 female, 2 did not indicate gender) at the Tilburg Central train station voluntarily participated on December 20, 2012. They were randomly assigned to the reminded (n = 39) or non-reminded (n = 39) condition.
Materials and procedure. We used the same procedure as in Study 1a, but subjects received all instructions and questions in paper-and-pencil format. The insurance reminder required them to indicate the name of their health insurance plan and whether they had additional coverage. Subjects then rated the extent to which they were satisfied with their medical insurance on a scale ranging from 1 = “unsatisfied” to 5 = “very satisfied”.
The reminder was either preceded or followed by seven questions. This time subjects answered exactly the same three health questions reported in Reference Tversky and KahnemanTykocinski (2008). Subjects rated the probability that, during the next five years, they would undergo a serious operation, would require physiotherapy, or would be in need of comprehensive nursing care. In addition, we asked them to rate the probability of two positive and two negative events. Specifically, subjects rated the probability that the current government would fall prematurely, that they would win the lottery within the next five years, that a European country would go bankrupt within five years, and that a Dutch person would win the Nobel Peace prize within five years. All questions were answered on scales ranging from 1 = “very small” to 5 = “very large”.Footnote 2
3.2 Results
Fifteen subjects did not indicate the name of their health insurers and were excluded from the analyses. Fifty (64.1%) indicated that they had some form of additional coverage. Mean satisfaction level was 3.84 (SD = 0.89) and there was no significant difference in satisfaction level between the reminded (M = 3.70, SD = 0.79) and non-reminded condition (M = 3.91, SD = 0.89), F(1, 60) = 0.919, p = .342, η2 = .015.Footnote 3
Confirmatory analyses. Mean evaluations of the probability of seven future events are shown in Table 2, along with univariate analyses of variance per item. The three health-related items were analyzed in a repeated-measures design with the reminder condition (reminded and non-reminded) as a between-subjects factor. Again, subjects who were reminded of their health insurance before they were asked about their likelihood of health problems did not differ in their ratings from those people who were reminded afterwards, F(1, 60) = 2.75, p = .103, η2 = .044. If anything, the insurance reminder somewhat increased rather than decreased the probability ratings.Footnote 4
Table 2: Means, standard deviations, sample sizes, and test statistics for all probability ratings of future events in Study 1b per condition.
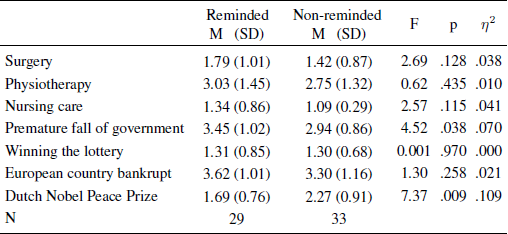
Exploratory analyses. The age range of our subjects (16–74 years) is broader than that in Reference Tversky and KahnemanTykocinski’s (2008) Experiment 1 (25–55 years) but it is possible that on average, she happened to recruit more older subjects than we did (mean age was not reported). If older individuals have stronger associations with insurance or are more concerned about negative health events, the protection effect might only occur in the older adults in our sample. To test this possibility, we included age as a covariate in the repeated-measures ANOVA and found that the probability ratings of the three events increased with age F(1, 58) = 4.92, p = .030, η2 = .061. However, there was no effect of reminder condition, F(1, 58) = 0.53, p = .473, η2 = .009. There was an almost-significant interaction effect between condition and age F(1, 58) = 2.97, p = .090, η2 = .049. In a regression analysis where the reminded condition was coded as 1 and the non-reminded condition as 0, the coefficient for the interaction term (reminder x age) was positive but not significant for every item (βsurgery = .505, t = 1.75, p = .086, βphysiotherapy = .257, t = 0.87, p = .388, βcomprehensive nursing care = .339, t = 1.19, p = .239). The same analysis on a variable that is the sum of the three probability ratings paints a similar picture, β = .485, t = 1.72, p = .090. This indicates that, the older people were, the more likely probability ratings were to go up after the reminder. This is the opposite of the effect reported in Reference Tversky and KahnemanTykocinski (2008) Study 1.
We also tested whether the effect of being reminded of insurance on probability evaluations was different for men and women, but we found no main effect of gender, F(1, 57) = 1.07, p = .306 η2 = .018, and no gender × condition interaction, F(1, 57) = 0.04, p = .850, η2 = .001.
In the current replication debate (e.g., Asendorpf et al., 2012), it has been suggested that variation in effects sizes may provide theoretical insights in the long run (IJzerman, Brandt, & van Wolferen, in press). Therefore, we should run tests that have enough power to detect effect sizes that are smaller than the ones originally reported. In Study 1c, we determined that we needed 150 subjects to have 95% power to find an effect that was half the size (η2 = .065, cohen’s f = 0.26) of the originally reported effect size. However, if we would run 400 subjects we would have 95% power to find an effect with cohen’s f = 0.16 (η2 ≈ .025) and 80% power to find an effect with cohen’s f = 0.12 (η2 ≈ .015). So we decided to recruit 400 subjects on Amazon Mechanical Turk (MTURK).
4 Study 1c: Reference Tversky and KahnemanTykocinski (2008) Exp. 1 on MTURK
4.1 Method
Subjects. Four hundred and three subjects completed the study on MTURK (M age= 26.81, range 18–63; 136 female) in exchange for $0.10 on December 3 and 4, 2012. People could only participate if they had an approval rate that was greater than 95% and if they lived in the U.S.Footnote 5
Materials and procedure. We included an instructional manipulation check (IMC) to weed out inattentive subjects (see Reference Oppenheimer, Meyvis and DavidenkoOppenheimer, Meyvis, & Davidenko, 2009). Subjects were excluded from the study if they did not successfully pass the IMC. Five hundred and three people started the survey, 411 (81.71%) passed the IMC and 8 subjects did not finish, so we were left with 403 subjects with complete data.
We used the same procedure as in Study 1a and 1b. All instructions and questions were presented in subjects’ web browsers using online survey software (Qualtrics). The insurance reminder required them to indicate the name of their health insurance plan and whether they had additional coverage. Subjects then rated the extent to which they were satisfied with their medical insurance on a scale ranging from 1 = “not satisfied at all” to 5 = “completely satisfied”.
The reminder was either preceded or followed by seven questions. Subjects answered exactly the same three health questions reported in Reference Tversky and KahnemanTykocinski (2008), rating the probability that during the next five years they would undergo a serious operation, would require physiotherapy, or would be in need of comprehensive nursing care. In addition, they rated the probability that within next five years they would lose a large amount of money, that Europe would go to war, that they would win the lottery, and that Israel and Palestine would sign a peace treaty. All questions were answered on scales ranging from 1 = “almost zero” to 5 = “very high probability”. Note that the questions and scale labels are exactly the same as reported in Reference Tversky and KahnemanTykocinski (2008).
4.2 Results
Unlike Israel or the Netherlands, not everyone in the U.S. has health insurance. Therefore, we coded whether subjects indicated the name of their health insurance companies. Forty-nine (12.16%) did not list a health insurance plan name or indicated that they had none. We exclude the people without health insurance from the analyses we report here, but the results are nearly the same when we include these people.
Fifty-six (13.90%) indicated that they had some form of additional coverage. Mean satisfaction level was 3.63 (SD = 0.92) and there was no significant difference in satisfaction level between the reminded (M = 3.63, SD = 0.89) and non-reminded condition (M = 3.61, SD = 0.95), F(1, 352) = 0.07, p = .794, η2 < .001.
Confirmatory analysis. Mean evaluations of the probability of seven future events are shown in Table 3. The three health-related items were analyzed in a repeated-measures design with the reminder condition (reminded and non-reminded) as a between-subjects factor. Again, subjects who were reminded of their health insurance before they were asked about their likelihood of health problems did not differ in their ratings from those people who were reminded afterwards, F(1, 352) < 0.01, p = .996, η2 < .001.Footnote 6
Table 3 Means, standard deviations, sample sizes, and test statistics for all probability ratings of future events in Study 1c per condition for people with health insurance.
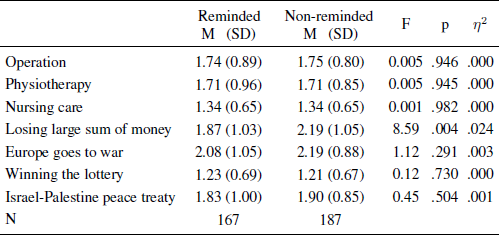
Exploratory analyses. The size of this sample allowed a better test of whether the protection effect interacts with age, as suggested in Study 1b. We included age as a covariate in the repeated-measures ANOVA and found that the probability ratings of the three events increased with age F(1, 350) 12.85, p < .001, η2 = .035. However, there was no effect of reminder condition, F(1, 350) = 0.93, p = .334, η2 = .003 and no age × condition interaction, F (1, 350) = 0.98, p = .324, η2 = .003.
We also tested whether the effect of being reminded of insurance on probability evaluations was different for men and women, but we did not find an interaction effect, F(1, 350) = 0.11, p = .915, η2 < .001. There was a small main effect of gender: Women rated the three negative health events as slightly more likely, F(1, 350) = 4.54, p = .034, η2 = .013.
The attentive reader will have noticed that we find some significant effects on the two positive and negative events that are not related to the health care. A reminder of health insurance led subjects in Study 1a to think war was less likely. In 1b, a premature fall of the government seemed more likely and a Dutch Nobel prize less likely after an insurance reminder. In 1c, subjects who were reminded of their insurance thought they were less likely to lose a large sum of money. Some of these apparent findings remain significant even after Bonferonni corrections. We believe these are examples of Type-1 errors but leave it to other researchers—who might have reason to believe these effects are real—to test whether they replicate.
In three separate studies, we were thus unable to replicate the protection effect reported in Experiment 1 by Reference Tversky and KahnemanTykocinski (2008). This failure to replicate was not due to insufficient power: In Study 1a, we had 76% power to find an effect as large as that reported by Tykocinski; in Study 1b, we had 95% power to detect such an effect, and in Study 1c we had 95% power to find an effect half the size of the originally reported effect. Our failure to replicate Tykocinski is also unlikely to be due to the use of undergraduate subjects, as Studies 1b and 1c used older subjects. However, the skeptical reader might feel that we are incapable of properly running experiments and that this explains our repeated failure to replicate the protection effect. (The first author readily admits that this thought crossed his mind as well.) In the following study we therefore attempted to test the tempting fate and protection effect hypotheses simultaneously. Specifically, we replicated the two “self” conditions of Experiment 2 reported in Reference Risen and GilovichRisen and Gilovich (2008), which tests whether students believe that they are especially likely to be called on to answer a question in class if they have not done the required reading. We also added a condition in which we attempted to conceptually replicate the protection effect. In this condition, subjects were asked to imagine that they had prepared extraordinarily well. If, as the protection effect hypothesis holds, making precautions salient primes a feeling of safety that makes negative events seem less likely, subjects in this condition should think it less likely that they will be called on to answer a question.
5 Study 2a: Reference Risen and GilovichRisen & Gilovich (2008) Exp. 2 + protection effect
5.1 Method
Subjects. One hundred thirty-three Fontys University at Tilburg students (93 female; M age= 20.08; range = 17–28; 1 did not indicate age) participated in a 20-minute session of unrelated experiments that ran for 2 days in November 2011 in exchange for 4 Euros. They were assigned to either the “prepared” (n = 46), “did not prepare” (n = 42), or “prepared really well” (n = 45) conditions.
Materials and procedure. The experiment was programmed in Authorware 7.0 and subjects read on a computer screen that they were to imagine the following situation:
You are taking a course and you are in a work group with approximately 20 students. This work group weekly discusses a piece of text or an article. Everyone should read and understand the article prior to the work group at home.
In the “prepared” condition subjects then read:
Like you do every week, you have read and understood the article reasonably well.
The “did not prepare” condition was designed to make subjects feel like they were tempting fate and therefore they read:
You did not really have that much time this week so you chose to not do your homework once. You thus do not really know what the article is about.
The “prepare really well” condition was designed to make subjects feel like had taken extra precautions and therefore they read:
You prepared really well this week. You read the article thoroughly twice and you even moved some appointments to make sure you had enough time to prepare for the lecture.
Subjects in all conditions then read the following:
This time, the teacher decides he will call on someone to publicly summarize the article in front of the group.
Subjects then rated the probability that the teacher would call upon them on a scale ranging from 1 = “very small chance” to 10 = “very large chance”.Footnote 7
5.2 Results
Confirmatory analysis.
Subjects who imagined that they did not prepare for the lecture only thought it was slightly more likely (M = 6.19, SD = 2.04) that they would be called upon to publicly summarize the article than did those who imagined preparing (M = 5.24, SD = 1.84) or preparing especially well (M = 5.24, SD = 2.00), F(2, 133) = 3.37, p = .037, η2 = .049. Post-hoc tests (LSD) indicated that the “did not prepare” condition differed from the other conditions (p prepare = .025 and p prepare really well = .026) whereas the “prepare” and “prepare really well” did not differ from each other, p = .990.
Exploratory analyses. In this study, we again tested for main- and interaction-effects of gender on the probability ratings but found neither, F main(1, 133) = 2.87, p = .092, η2 = .022, F interaction(2, 133) = 0.33, p = .717, η2 = .005. Perhaps because of a relatively restricted range of age, we do not find a very strong effect of age, F(1, 132) = 3.07, p = .082, η2 = .024, or an interaction effect with age, F(1, 132) = 1.57, p = .212, η2 = .024.
We thus replicated the tempting fate effect reported in Experiment 1 by Reference Risen and GilovichRisen and Gilovich (2008). We added a condition in which people prepared especially well for the lecture to test whether this would lead to a protection effect. However, as one of the reviewers on a previous version of this article pointed out, we might not have given the protection effect a fair chance. Our control condition mentions preparation, while our protection effect condition mentions “preparing really well”. The difference between these two conditions is not very large and a control condition that does not mention preparation at all might be better. Therefore, in Study 2b we replicated Study 2a but altered the control condition so that it did not remind subjects of preparation at all.
6 Study 2b: Study 2a with a different control condition
Using G*Power we determined that we would need 251 people to find an effect as large as we did in Study 2a (η2 = .049, Cohen’s f = 0.23). To this end, we sent out the survey to 460 second-year undergraduate students—who had completed the third author’s course 2 months earlier—on December 5th and closed the survey December 17 (although the last subject finished December 13). We also ran the study in the lab (which recruits from a different subject pool) between December 10 and December 14, 2012.
6.1 Method
Subjects. One hundred and eighty five people (40.2%) responded to the email and filled out the survey. One hundred and eighteen people participated in the lab; combining the lab and online responses yielded complete data for 292 people (M age=20.6; range 18–36; 200 female). They were randomly assigned to the control (n = 97), tempting fate (n = 99), or the protection effect conditions (n = 96).
Materials and procedure. We included an instructional manipulation check (IMC) to weed out inattentive subjects (Reference Oppenheimer, Meyvis and DavidenkoOppenheimer, Meyvis, & Davidenko, 2009). Subjects could repeat the IMC if they failed to complete it successfully, but were automatically excluded from the study if they failed 4 times. However, every subject successfully passed before reaching the exclusion point.
The materials were identical to those of Study 2b with two exceptions. The survey was programmed in Qualtrics and we deleted the last sentence of the text that everyone read to ensure that the people in the control condition did not think about preparation for the class. The new text read:
You are taking a course and you are in a work group with approximately 20 students. This work group weekly discusses a piece of text or an article.
In the control condition there was no additional text, while the other two conditions displayed the exact same text as in Study 2a.
We asked people to indicate where they filled out the survey (in the lab vs. at home or “other place”) and at the end of the survey we asked people to indicate what the text they read said about preparation for class (“no preparation”, “very good preparation”, “no mention of preparation”, or “don’t know”). We included only people who passed this manipulation check (96.6%) and who took more than 10 seconds to read the text and answer the question (95.9%). In total we excluded 20 subjects (6.8%) and ran the analyses on the complete data of 271 subjects.
6.2 Results
Confirmatory analysis. Subjects who imagined that they did not prepare for the lecture did not think it was more likely (M = 5.04, SD = 2.12) that they would be called upon to publicly summarize the article than did those who imagined preparing really well (M = 4.56, SD = 1.65) or who were not reminded of preparing at all (M = 4.71, SD = 2.10), F(2, 272) = 1.49, p = .227, η2 = .011.Footnote 8 Note that directional (one-tailed) tests of the tempting fate and protection effect support only the tempting fate effect, t temptfate−protection (171.99)= −1.74, p = .042, t temptfate−control (175) = −1.06, p = .144, t control−protection (159.42) = .52, p = .301. So, we find weaker evidence for the tempting fate effect than in Study 2a and find no support for the protection effect.
Exploratory analyses. We looked for main and interaction effects of age but found neither, F main(1, 271) = 1.35, p = .589, η2 = .004, F interaction(2, 271) = 0.40, p = .674, η2 = .003. Unexpectedly, we found a large difference in probability ratings between men and women, F(1, 272) = 27.66, p < .001, η2 = .094, such that men thought they were less likely to be called upon (M = 3.85, SD = 2.13) than women do (M = 5.15, SD = 1.76). In addition, we found a significant interaction effect, F(2, 272) = 3.37, p = .036, η2 = .025.
To explore this interaction effect we ran the ANOVA reported under “confirmatory analysis” above separately for men and women. For men, it is clear that there is no difference between the control (M = 3.86, SD = 2.33, n = 29), tempting fate (M = 3.56, SD = 1.95, n = 27), and protection effect conditions (M = 4.17, SD = 2.12, n = 24), F(2, 80) = 0.52, p = .598, η2 = .013. Directional (one-tailed) tests do also not provide evidence for either effect, t temptfate−protection (49)= 1.07, p = .144, t temptfate−control (54) = .53, p = .299, t control−protection (51) = −.49, p = .312.
For women however, we replicate the findings reported in Reference Risen and GilovichRisen and Gilovich (2008). Women who imagined that they did not prepare for the lecture thought it was more likely (M = 5.66, SD = 1.88, n = 65) that they would be called upon to publicly summarize the article than did those who imagined preparing really well (M = 4.69, SD = 1.46, n = 71) or who were not reminded of preparation at all (M = 5.14, SD = 1.84, n = 56), F(2, 192) = 5.38, p = .005, η2 = .054. Post-hoc tests (LSD) indicated that the tempting fate condition differed from the protection effect condition (p = .001) but not from the control condition (p = .101). The control condition and the protection effect condition also did not differ from each other (p = .144).
Following these analyses we checked with the authors of the original tempting fate paper but unfortunately, age and gender were not recorded in the experiments reported in Reference Risen and GilovichRisen and Gilovich (2008). We are not entirely certain what to make of this interaction-effect with gender. From personal experience with teaching female undergraduates we do think that they are more worried than male undergraduates about making public statements in front of class and we might have had insufficient power to detect this interaction in Study 2a. Following Reference Risen and GilovichRisen and Gilovich (2007, 2008), people who can more easily imagine negative outcomes should be more likely to display a belief in tempting fate. The entirely post-hoc explanation that women can more easily imagine being embarrassed in front of class, and are therefore more susceptible to this specific demonstration of the tempting fate effect, is one that could be tested in future research.
7 Discussion
In three studies, we attempted to replicate the protection effect reported in Reference Tversky and KahnemanTykocinski’s (2008) Experiment 1 as closely as possible. Using a student sample, a sample of train commuters (as in the original study), and a large online U.S. sample, we did not find evidence for this effect. In a follow-up study in which we tried to conceptually replicate the protection effect we also did not find support for it. However, we did find evidence supportive of a belief in tempting fate.
7.1 Why did the protection effect not replicate?
One possible reason for our failure to replicate Reference Tversky and KahnemanTykocinski’s (2008) Experiment 1 is that risk may be a more salient factor in the daily lives of Israelis, compared to our Dutch and American subjects. Israel has a recent history of war, and today, bombings in public places and military conflict are still common. This might make Israelis more attuned to risk, and more sensitive to variations in it. If so, they might also be more susceptible to features of life that seemingly decrease the probability of misfortune (i.e., they are more sensitive to the protection effect). But note that there are also important similarities between those countries. Both Israel and the Netherlands require residents to purchase health insurance (and have done so for many years). In addition, before health insurance became compulsory in 1995 most Israelis also had health insurance (Israel Ministry of Foreign Affairs, 2002). Furthermore, in the U.S. sample (where health insurance is much less of a default than in Israel and the Netherlands), we also do not find evidence for the protection effect. Differences in how unusual health insurance is thus seem unlikely explanations for the differences in the findings we report and those in Reference Tversky and KahnemanTykocinski (2008).
There might of course be cultural differences in the extent to which people in different countries are susceptible to magical thinking effects in general (in this case, possibly because of a difference of risk-salience in the daily lives of the populations in question). However, we do find another form of magical thinking in Study 2a and 2b. This still leaves the possibility that the protection effect is more likely to happen in Israel than it is in the U.S. or the Netherlands, but that all populations are susceptible to tempting fate effects. This could be tested by simultaneously rerunning our Study 2b in Israel and the Netherlands.
A final possibility is that the protection effect reported in Reference Tversky and KahnemanTykocinski (2008) was merely due to chance. The conventional alpha levels do allow for 5% false-positives and it is possible that this study “accidentally” found a protection effect. The only real test of this possibility is to rerun the exact same study in Israel to see if the effect replicates.
7.2 Why attempt “direct” replications?
In light of recent discussions with respect to robustness of effects reported in the (social) psychological literature (Open Science Collaboration, unpublished manuscript; Reference Simmons, Nelson and SimonsohnSimmons et al., 2011) we feel it is important to point out that we did not just randomly pick one article to see if it replicates. We were (and are) genuinely interested in the protection effect as we thought that the insurance protection effect might be one of the causes of the moral hazard effect (i.e., insurance leads people to take more risk, Arrow, 1963). When we failed to replicate the original effect study reported in Reference Tversky and KahnemanTykocinski (2008) we tried harder to find evidence for the protection effect. As is clear from this paper, these efforts did not yield positive results.
Our attempt to replicate the tempting fate effect reported in Reference Risen and GilovichRisen and Gilovich (2008) was aimed at testing whether we could find a different magical thinking effect. This would rule out the possibility that the Dutch are simply not sensitive to magical thinking effects. We thus think that the successful replication of the tempting fate effect adds credibility to the non-replication of the protection effect.
On a broader level, we think it is valuable to run direct replications to test the robustness and universality (i.e., cross-cultural robustness) of an effect. Initiatives like http://www.psycfiledrawer.org (see Reference CarpenterCarpenter, 2012) are a good start, but devoting some journal space to replication attempts seems valuable as well. In fact, many have argued that, without direct replication, scientific progress is difficult if not impossible (e.g., Reference Feynman and LeightonFeynmann & Leighton, 1997). In addition to direct replications, conceptual replications are important to test the generality of an effect and test its reliance on a specific method or paradigm (Nussbaum, 2012; IJzerman, et al., in press). Here, of course, we report both: three direct replications (Studies 1a, 1b, and 1c) and two conceptual replications (Study 2a and 2b).
Finally, we stress that our failed replications do not necessarily mean that the protection effect reported in Reference Tversky and KahnemanTykocinski (2008) does not exist. We merely report that we cannot replicate this finding in the Netherlands, and that a conceptual replication also does not provide evidence for the existence of the protection effect. Future replication attempts will prove valuable, especially when aimed at detecting possible moderators that might explain our failure to replicate the protection effect.
Appendix: Full design of study 1a
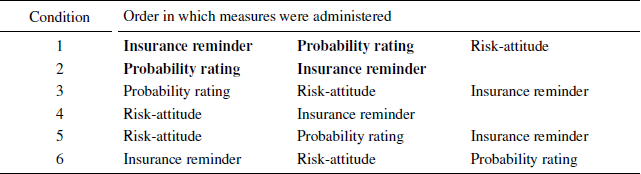
Insurance reminder = 3 questions related to insurance described in Study 1a. Probability rating = the 7 probability ratings described in Study 1a. Risk attitude = Translated version of the domain-specific risk-attitude scale (Reference Weber, Blais and BetzWeber, Blais, & Betz, 2002). Measures in bold underlined font are reported in the paper.




