Article contents
UNIQUENESS OF THE WELDING PROBLEM FOR SLE AND LIOUVILLE QUANTUM GRAVITY
Published online by Cambridge University Press: 05 July 2019
Abstract
We give a simple set of geometric conditions on curves  $\unicode[STIX]{x1D702}$,
$\unicode[STIX]{x1D702}$, 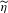 $\widetilde{\unicode[STIX]{x1D702}}$ in
$\widetilde{\unicode[STIX]{x1D702}}$ in 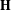 $\mathbf{H}$ from
$\mathbf{H}$ from  $0$ to
$0$ to 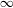 $\infty$ so that if
$\infty$ so that if 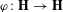 $\unicode[STIX]{x1D711}:\mathbf{H}\rightarrow \mathbf{H}$ is a homeomorphism which is conformal off
$\unicode[STIX]{x1D711}:\mathbf{H}\rightarrow \mathbf{H}$ is a homeomorphism which is conformal off  $\unicode[STIX]{x1D702}$ with
$\unicode[STIX]{x1D702}$ with 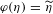 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702})=\widetilde{\unicode[STIX]{x1D702}}$ then
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702})=\widetilde{\unicode[STIX]{x1D702}}$ then  $\unicode[STIX]{x1D711}$ is a conformal automorphism of
$\unicode[STIX]{x1D711}$ is a conformal automorphism of 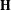 $\mathbf{H}$. Our motivation comes from the fact that it is possible to apply our result to random conformal welding problems related to the Schramm–Loewner evolution (SLE) and Liouville quantum gravity (LQG). In particular, we show that if
$\mathbf{H}$. Our motivation comes from the fact that it is possible to apply our result to random conformal welding problems related to the Schramm–Loewner evolution (SLE) and Liouville quantum gravity (LQG). In particular, we show that if  $\unicode[STIX]{x1D702}$ is a non-space-filling
$\unicode[STIX]{x1D702}$ is a non-space-filling 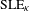 $\text{SLE}_{\unicode[STIX]{x1D705}}$ curve in
$\text{SLE}_{\unicode[STIX]{x1D705}}$ curve in 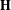 $\mathbf{H}$ from
$\mathbf{H}$ from  $0$ to
$0$ to 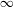 $\infty$, and
$\infty$, and  $\unicode[STIX]{x1D711}$ is a homeomorphism which is conformal on
$\unicode[STIX]{x1D711}$ is a homeomorphism which is conformal on 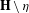 $\mathbf{H}\setminus \unicode[STIX]{x1D702}$, and
$\mathbf{H}\setminus \unicode[STIX]{x1D702}$, and 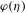 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702})$,
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702})$,  $\unicode[STIX]{x1D702}$ are equal in distribution, then
$\unicode[STIX]{x1D702}$ are equal in distribution, then  $\unicode[STIX]{x1D711}$ is a conformal automorphism of
$\unicode[STIX]{x1D711}$ is a conformal automorphism of 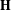 $\mathbf{H}$. Applying this result for
$\mathbf{H}$. Applying this result for  $\unicode[STIX]{x1D705}=4$ establishes that the welding operation for critical (
$\unicode[STIX]{x1D705}=4$ establishes that the welding operation for critical (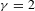 $\unicode[STIX]{x1D6FE}=2$) LQG is well defined. Applying it for
$\unicode[STIX]{x1D6FE}=2$) LQG is well defined. Applying it for 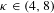 $\unicode[STIX]{x1D705}\in (4,8)$ gives a new proof that the welding of two independent
$\unicode[STIX]{x1D705}\in (4,8)$ gives a new proof that the welding of two independent 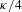 $\unicode[STIX]{x1D705}/4$-stable looptrees of quantum disks to produce an
$\unicode[STIX]{x1D705}/4$-stable looptrees of quantum disks to produce an 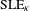 $\text{SLE}_{\unicode[STIX]{x1D705}}$ on top of an independent
$\text{SLE}_{\unicode[STIX]{x1D705}}$ on top of an independent 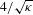 $4/\sqrt{\unicode[STIX]{x1D705}}$-LQG surface is well defined.
$4/\sqrt{\unicode[STIX]{x1D705}}$-LQG surface is well defined.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2019
References
- 6
- Cited by


