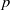 $p$-adic
$p$-adic 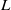 $L$-functions at near-central points
$L$-functions at near-central pointsPublished online by Cambridge University Press: 24 September 2013
Using the 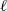 $\ell $-invariant constructed in our previous paper we prove a
Mazur–Tate–Teitelbaum-style formula for derivatives of
$\ell $-invariant constructed in our previous paper we prove a
Mazur–Tate–Teitelbaum-style formula for derivatives of 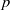 $p$-adic
$p$-adic 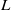 $L$-functions of modular forms at trivial zeros. The novelty of this
result is to cover the near-central point case. In the central point case our formula
coincides with the Mazur–Tate–Teitelbaum conjecture proved by Greenberg and Stevens
and by Kato, Kurihara and Tsuji at the end of the 1990s.
$L$-functions of modular forms at trivial zeros. The novelty of this
result is to cover the near-central point case. In the central point case our formula
coincides with the Mazur–Tate–Teitelbaum conjecture proved by Greenberg and Stevens
and by Kato, Kurihara and Tsuji at the end of the 1990s.