Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-27T06:49:31.171Z Has data issue: false hasContentIssue false
  • English
  • Français

SPECTRAL INEQUALITIES FOR COMBINATIONS OF HERMITE FUNCTIONS AND NULL-CONTROLLABILITY FOR EVOLUTION EQUATIONS ENJOYING GELFAND–SHILOV SMOOTHING EFFECTS

Part of: Controllability, observability, and system structure Nontrigonometric harmonic analysis Close-to-elliptic equations and systems

Published online by Cambridge University Press:  21 March 2022

Jérémy Martin  and
Karel Pravda-Starov Open the ORCID record for Karel Pravda-Starov [Opens in a new window]
Jérémy Martin
Affiliation:
Univ Rennes, CNRS, IRMAR-UMR 6625, F-35000 Rennes, France (jeremy.martin@ens-rennes.fr)
Karel Pravda-Starov*
Affiliation:
Univ Rennes, CNRS, IRMAR-UMR 6625, F-35000 Rennes, France
*
karel.pravda-starov@univ-rennes1.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

This work is devoted to the study of uncertainty principles for finite combinations of Hermite functions. We establish some spectral inequalities for control subsets that are thick with respect to some unbounded densities growing almost linearly at infinity, and provide quantitative estimates, with respect to the energy level of the Hermite functions seen as eigenfunctions of the harmonic oscillator, for the constants appearing in these spectral estimates. These spectral inequalities allow us to derive the null-controllability in any positive time for evolution equations enjoying specific regularizing effects. More precisely, for a given index 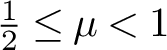$\frac {1}{2} \leq \mu <1$, we deduce sufficient geometric conditions on control subsets to ensure the null-controllability of evolution equations enjoying regularizing effects in the symmetric Gelfand–Shilov space 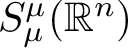$S^{\mu }_{\mu }(\mathbb {R}^{n})$. These results apply in particular to derive the null-controllability in any positive time for evolution equations associated to certain classes of hypoelliptic non-self-adjoint quadratic operators, or to fractional harmonic oscillators.

Keywords

uncertainty principlesLogvinenko–Sereda-type estimatesHermite functionsnull-controllabilityquadratic equationsfractional harmonic oscillatorsGelfand–Shilov regularity

MSC classification

Primary: 93B05: Controllability
Secondary: 42C05: Orthogonal functions and polynomials, general theory 35H10: Hypoelliptic equations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 6 , November 2023 , pp. 2533 - 2582
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, R. A. and Fournier, J. J. F., Sobolev Spaces, 2nd ed., Pure and Applied Mathematics (Amsterdam), 140 (Elsevier/Academic Press, Amsterdam, 2003).Google Scholar
Alphonse, P. and Bernier, J., ‘Polar decomposition of semigroups generated by non-selfadjoint quadratic differential operators and regularizing effects’, Preprint, 2021, https://arxiv.org/abs/1909.03662; forthcoming in Ann. Sci. Éc. Norm. Supér. (4).Google Scholar
Amit, T. and Olevskii, A., ‘On the annihilation of thin sets’, Preprint, 2017, https://arxiv.org/abs/1711.04131.Google Scholar
Amrein, W. O. and Berthier, A. M., On support properties of ${L}^p$ -functions and their Fourier transforms, J. Funct. Anal. 24(3) (1977), 258–267.CrossRefGoogle Scholar
Artin, E., The Gamma Function, transl. Butler, Michael, Athena Series: Selected Topics in Mathematics (Holt, Rinehart and Winston, New York, 1964).Google Scholar
Beauchard, K., Egidi, M. and Pravda-Starov, K., Geometric conditions for the null-controllability of hypoelliptic quadratic parabolic equations with moving control supports, C. R. Math. Acad. Sci. Paris 358(6) (2020), 651–700.Google Scholar
Beauchard, K., Jaming, P.and Pravda-Starov, K., Spectral inequality for finite combinations of Hermite functions and null-controllability of hypoelliptic quadratic equations, Studia Math. 260(1) (2021), 1–43.CrossRefGoogle Scholar
Beauchard, K. and Pravda-Starov, K., Null-controllability of hypoelliptic quadratic differential equations, J. Éc. polytech. Math. 5 (2018), 1–43.CrossRefGoogle Scholar
Benedicks, M., On Fourier transforms of functions supported on sets of finite Lebesgue measure, J. Math. Anal. Appl. 106(1) (1985), 180–183.CrossRefGoogle Scholar
Bourgain, J. and Dyatlov, S., Fourier dimension and spectral gaps for hyperbolic surfaces, Geom. Funct. Anal. 27 (2017), 744–771.CrossRefGoogle Scholar
Bourgain, J. and Dyatlov, S., Spectral gaps without the pressure condition, Ann. of Math. (2) 187(3) (2018), 825–867.CrossRefGoogle Scholar
Coron, J.-M., Control and Nonlinearity, Mathematical Surveys and Monographs, 136 (American Mathematical Society, Providence, RI, 2007).Google Scholar
Demange, B., Uncertainty principles associated to non-degenerate quadratic forms, Mém. Soc. Math. Fr. 119(2009), 98 (2010).Google Scholar
Dyatlov, S. and Jin, L., Dolgopyat’s method and the fractal uncertainty principle, Anal. PDE 11(6) (2018), 1457–1485.CrossRefGoogle Scholar
Egidi, M. and Veselić, I., Sharp geometric condition for null-controllability of the heat equation on ${\mathbb{R}}^d$ and consistent estimates on the control cost, Arch. Math. (Basel) 111(1) (2018), 85–99.CrossRefGoogle Scholar
Gelfand, I. M. and Shilov, G. E., Generalized Functions II (Academic Press, New York, 1968).Google Scholar
Gramchev, T., Pilipović, S. and Rodino, L., Classes of degenerate elliptic operators in Gelfand-Shilov spaces, in New Developments in Pseudo-Differential Operators, Operator Theory: Advances and Applications, 189, pp. 15-31 (Birkhäuser, Basel, 2009).Google Scholar
Hitrik, M. and Pravda-Starov, K., Spectra and semigroup smoothing for non-elliptic quadratic operators, Math. Ann. 344(4) (2009), 801–846.CrossRefGoogle Scholar
Hitrik, M. and Pravda-Starov, K., Semiclassical hypoelliptic estimates for non-selfadjoint operators with double characteristics, Comm. Partial Differential Equations 35(6) (2010), 988–1028.CrossRefGoogle Scholar
Hitrik, M. and Pravda-Starov, K., Eigenvalues and subelliptic estimates for non-selfadjoint semiclassical operators with double characteristics, Ann. Inst. Fourier (Grenoble) 63(3) (2013), 985–1032.CrossRefGoogle Scholar
Hitrik, M., Pravda-Starov, K. and Viola, J., Short-time asymptotics of the regularizing effect for semigroups generated by quadratic operators, Bull. Sci. Math. 141(7) (2017), 615–675.CrossRefGoogle Scholar
Hitrik, M., Pravda-Starov, K. and Viola, J., From semigroups to subelliptic estimates for quadratic operators, Trans. Amer. Math. Soc. 370(10) (2018), 7391–7415.CrossRefGoogle Scholar
Hörmander, L., The Analysis of Linear Partial Differential Operators I, 2nd ed., Grundlehren der Mathematischen Wissenschaften, 256 (Springer-Verlag, Berlin, 1990).Google Scholar
Hörmander, L., Symplectic classification of quadratic forms and general Mehler formulas, Math. Z. 219(3) (1995), 413–449.CrossRefGoogle Scholar
Jaming, P., Nazarov’s uncertainty principles in higher dimension, J. Approx. Theory 149 (2007), 30–41.CrossRefGoogle Scholar
Kovrijkine, O., Some results related to the Logvinenko-Sereda Theorem, Proc. Amer. Math. Soc. 129( 10) (2001), 3037–3047.CrossRefGoogle Scholar
Kovrizhkin, O., The uncertainty principle for certain densities, Int. Math. Res. Not. IMRN 2003(17) (2003), 933–951.CrossRefGoogle Scholar
Lions, J.-L., Contrôlabilité exacte, perturbations et stabilisation de systèmes distribués, Tome 1 et 2, Recherches in Mathématiques Appliquées, 8 (Masson, Paris, 1988).Google Scholar
Logvinenko, V. N. and Sereda, J. F., Equivalent norms in spaces of entire functions of exponential type, Teor. Funkcii Funkcional. Anal. i Prilozen. Vyp. 20 (1974), 102–111, 175.Google Scholar
Miller, L., A direct Lebeau-Robbiano strategy for the observability of heat-like semigroups, Discrete Contin. Dyn. Syst. Ser. B 14(4) (2010), 1465–1485.Google Scholar
Miller, L., Spectral Inequalities for the Control of Linear PDEs. PDE’s, dispersion, scattering theory and control theory, 81–98, Sémin. Congr., 30, Soc. Math. France, Paris, (2017).Google Scholar
Nazarov, F. L., Local estimates for exponential polynomials and their applications to inequalities of the uncertainty principle type, Algebra i Analiz 5 (1993), 3–66; translation in St. Petersburg Math. J. 5 (1994), 663–717.Google Scholar
Nicola, F. and Rodino, L., Global Pseudo-Differential Calculus on Euclidean Spaces, Pseudo-Differential Operators, Theory and Applications, 4 (Birkhäuser Verlag, Basel, 2010).CrossRefGoogle Scholar
Ottobre, M., Pavliotis, G. A. and Pravda-Starov, K., Exponential return to equilibrium for hypoelliptic quadratic systems, J. Funct. Anal. 262(9) (2012), 4000–4039.CrossRefGoogle Scholar
Pravda-Starov, K., Subelliptic estimates for quadratic differential operators, Amer. J. Math. 133(1) (2011), 39–89.CrossRefGoogle Scholar
Pravda-Starov, K., Rodino, L. and Wahlberg, P., Propagation of Gabor singularities for Schrödinger equations with quadratic Hamiltonians, Math. Nachr. 291 (2018), 128–159.CrossRefGoogle Scholar
Rudin, W., Real and Complex Analysis, 3rd ed. (McGraw-Hill Book Co., New York, 1987).Google Scholar
Shubin, C., Vakilian, R. and Wolff, T., Some harmonic analysis questions suggested by Anderson-Bernoulli models, Geom. Funct. Anal. 8 (1998), 932–964.CrossRefGoogle Scholar
Sjöstrand, J., Parametrices for pseudodifferential operators with multiple characteristics, Ark. Mat. 12 (1974), 85–130.CrossRefGoogle Scholar
Toft, J., Khrennikov, A., Nilsson, B. and Nordebo, S., Decompositions of Gelfand-Shilov kernels into kernels of similar class, J. Math. Anal. Appl. 396(1) (2012), 315–322.CrossRefGoogle Scholar
Tucsnak, M. and Weiss, G., Observation and Control for Operator Semigroups, Birkhäuser Advanced Texts: Basler Lehrbücher (Birkhäuser Verlag, Basel, 2009).CrossRefGoogle Scholar
Viola, J., Resolvent estimates for non-selfadjoint operators with double characteristics, J. Lond. Math. Soc. (2) 85(1) (2012), 41–78.CrossRefGoogle Scholar
Viola, J., Non-elliptic quadratic forms and semiclassical estimates for non-selfadjoint operators, Int. Math. Res. Not. IMRN 2013(20) (2013), 4615–4671.CrossRefGoogle Scholar
Viola, J., Spectral projections and resolvent bounds for partially elliptic quadratic differential operators, J. Pseudo-Differ. Oper. Appl. 4 (2013), 145–221.CrossRefGoogle Scholar
Wang, G., Wang, M., Zhang, C. and Zhang, Y., Observable set, observability, interpolation inequality and spectral inequality for the heat equation in ${\mathbb{R}}^n$ , J. Math. Pures Appl. (9) 126 (2019), 144–194.10.1016/j.matpur.2019.04.009CrossRefGoogle Scholar