Article contents
SMOOTH BIMODULES AND COHOMOLOGY OF II1 FACTORS
Published online by Cambridge University Press: 07 May 2015
Abstract
We prove that, under rather general conditions, the 1-cohomology of a von Neumann algebra 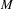 $M$ with values in a Banach
$M$ with values in a Banach  $M$ -bimodule satisfying a combination of smoothness and operatorial conditions vanishes. For instance, we show that, if
$M$ -bimodule satisfying a combination of smoothness and operatorial conditions vanishes. For instance, we show that, if 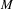 $M$ acts normally on a Hilbert space
$M$ acts normally on a Hilbert space 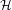 ${\mathcal{H}}$ and
${\mathcal{H}}$ and 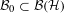 ${\mathcal{B}}_{0}\subset {\mathcal{B}}({\mathcal{H}})$ is a norm closed
${\mathcal{B}}_{0}\subset {\mathcal{B}}({\mathcal{H}})$ is a norm closed 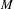 $M$ -bimodule such that any
$M$ -bimodule such that any 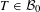 $T\in {\mathcal{B}}_{0}$ is smooth (i.e., the left and right multiplications of
$T\in {\mathcal{B}}_{0}$ is smooth (i.e., the left and right multiplications of  $T$ by
$T$ by 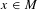 $x\in M$ are continuous from the unit ball of
$x\in M$ are continuous from the unit ball of 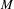 $M$ with the
$M$ with the 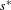 $s^{\ast }$ -topology to
$s^{\ast }$ -topology to 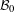 ${\mathcal{B}}_{0}$ with its norm), then any derivation of
${\mathcal{B}}_{0}$ with its norm), then any derivation of 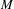 $M$ into
$M$ into 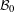 ${\mathcal{B}}_{0}$ is inner. The compact operators are smooth over any
${\mathcal{B}}_{0}$ is inner. The compact operators are smooth over any 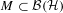 $M\subset {\mathcal{B}}({\mathcal{H}})$ , but there is a large variety of non-compact smooth elements as well.
$M\subset {\mathcal{B}}({\mathcal{H}})$ , but there is a large variety of non-compact smooth elements as well.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 1 , February 2017 , pp. 155 - 187
- Copyright
- © Cambridge University Press 2015
References
- 12
- Cited by

