Article contents
Simple wild 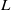 -packets
-packets
Published online by Cambridge University Press: 16 May 2012
Abstract
In a recent paper, Gross and Reeder study the arithmetic properties of discrete Langlands parameters for semi-simple 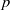 -adic groups, and they conjecture that a special class of these – the simple wild parameters – should correspond to
-adic groups, and they conjecture that a special class of these – the simple wild parameters – should correspond to 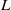 -packets consisting of simple supercuspidal representations. We provide a construction of this correspondence, and show that the simple wild
-packets consisting of simple supercuspidal representations. We provide a construction of this correspondence, and show that the simple wild 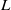 -packets satisfy many expected properties. In particular, they admit a description in terms of the Langlands dual group, and contain a unique generic element for a fixed Whittaker datum. Moreover, we prove their stability on an open subset of the regular semi-simple elements, and show that they satisfy a natural compatibility with respect to unramified base-change.
-packets satisfy many expected properties. In particular, they admit a description in terms of the Langlands dual group, and contain a unique generic element for a fixed Whittaker datum. Moreover, we prove their stability on an open subset of the regular semi-simple elements, and show that they satisfy a natural compatibility with respect to unramified base-change.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 1 , January 2013 , pp. 43 - 75
- Copyright
- Copyright © Cambridge University Press 2013
References
- 12
- Cited by

