Article contents
RECIPROCITY SHEAVES AND THEIR RAMIFICATION FILTRATIONS
Published online by Cambridge University Press: 19 March 2021
Abstract
We define a motivic conductor for any presheaf with transfers F using the categorical framework developed for the theory of motives with modulus by Kahn, Miyazaki, Saito and Yamazaki. If F is a reciprocity sheaf, this conductor yields an increasing and exhaustive filtration on 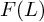 $F(L)$, where L is any henselian discrete valuation field of geometric type over the perfect ground field. We show that if F is a smooth group scheme, then the motivic conductor extends the Rosenlicht–Serre conductor; if F assigns to X the group of finite characters on the abelianised étale fundamental group of X, then the motivic conductor agrees with the Artin conductor defined by Kato and Matsuda; and if F assigns to X the group of integrable rank
$F(L)$, where L is any henselian discrete valuation field of geometric type over the perfect ground field. We show that if F is a smooth group scheme, then the motivic conductor extends the Rosenlicht–Serre conductor; if F assigns to X the group of finite characters on the abelianised étale fundamental group of X, then the motivic conductor agrees with the Artin conductor defined by Kato and Matsuda; and if F assigns to X the group of integrable rank 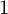 $1$ connections (in characteristic
$1$ connections (in characteristic 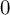 $0$), then it agrees with the irregularity. We also show that this machinery gives rise to a conductor for torsors under finite flat group schemes over the base field, which we believe to be new. We introduce a general notion of conductors on presheaves with transfers and show that on a reciprocity sheaf, the motivic conductor is minimal and any conductor which is defined only for henselian discrete valuation fields of geometric type with perfect residue field can be uniquely extended to all such fields without any restriction on the residue field. For example, the Kato–Matsuda Artin conductor is characterised as the canonical extension of the classical Artin conductor defined in the case of a perfect residue field.
$0$), then it agrees with the irregularity. We also show that this machinery gives rise to a conductor for torsors under finite flat group schemes over the base field, which we believe to be new. We introduce a general notion of conductors on presheaves with transfers and show that on a reciprocity sheaf, the motivic conductor is minimal and any conductor which is defined only for henselian discrete valuation fields of geometric type with perfect residue field can be uniquely extended to all such fields without any restriction on the residue field. For example, the Kato–Matsuda Artin conductor is characterised as the canonical extension of the classical Artin conductor defined in the case of a perfect residue field.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 1 , January 2023 , pp. 71 - 144
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 11
- Cited by


