Published online by Cambridge University Press: 22 January 2018
Let  $X$ be a quasi-compact and quasi-separated scheme. There are two fundamental and pervasive facts about the unbounded derived category of
$X$ be a quasi-compact and quasi-separated scheme. There are two fundamental and pervasive facts about the unbounded derived category of 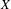 $X$: (1)
$X$: (1) 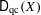 $\mathsf{D}_{\text{qc}}(X)$ is compactly generated by perfect complexes and (2) if
$\mathsf{D}_{\text{qc}}(X)$ is compactly generated by perfect complexes and (2) if 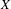 $X$ is noetherian or has affine diagonal, then the functor
$X$ is noetherian or has affine diagonal, then the functor 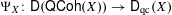 $\unicode[STIX]{x1D6F9}_{X}:\mathsf{D}(\mathsf{QCoh}(X))\rightarrow \mathsf{D}_{\text{qc}}(X)$ is an equivalence. Our main results are that for algebraic stacks in positive characteristic, the assertions (1) and (2) are typically false.
$\unicode[STIX]{x1D6F9}_{X}:\mathsf{D}(\mathsf{QCoh}(X))\rightarrow \mathsf{D}_{\text{qc}}(X)$ is an equivalence. Our main results are that for algebraic stacks in positive characteristic, the assertions (1) and (2) are typically false.
The first and second author are supported by the Australian Research Council (ARC), grant numbers FL100100137, DE150101799, and DP150102313. The third author is supported by the Swedish Research Council (VR), grant numbers 2011-5599 and 2015-05554.