Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bandman, Tatiana
Gordeev, Nikolai
Kunyavskiĭ, Boris
and
Plotkin, Eugene
2012.
Equations in simple Lie algebras.
Journal of Algebra,
Vol. 355,
Issue. 1,
p.
67.
Riche, Simon
2017.
Kostant section, universal centralizer, and a modular derived Satake equivalence.
Mathematische Zeitschrift,
Vol. 286,
Issue. 1-2,
p.
223.
Ganapathy, Radhika
and
Varma, Sandeep
2017.
ON THE LOCAL LANGLANDS CORRESPONDENCE FOR SPLIT CLASSICAL GROUPS OVER LOCAL FUNCTION FIELDS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 16,
Issue. 5,
p.
987.
Adler, Jeffrey D.
Fintzen, Jessica
and
Varma, Sandeep
2018.
On Kostant sections and topological nilpotence.
Journal of the London Mathematical Society,
Vol. 97,
Issue. 2,
p.
325.
Totaro, Burt
2018.
Hodge theory of classifying stacks.
Duke Mathematical Journal,
Vol. 167,
Issue. 8,
Biswas, Indranil
Chaput, Pierre-Emmanuel
and
Mourougane, Christophe
2019.
Stability of the Tangent Bundle of G/P in Positive Characteristics.
Algebras and Representation Theory,
Vol. 22,
Issue. 1,
p.
239.
GARIBALDI, SKIP
and
GURALNICK, ROBERT M.
2020.
GENERICALLY FREE REPRESENTATIONS II: IRREDUCIBLE REPRESENTATIONS.
Transformation Groups,
Vol. 25,
Issue. 3,
p.
793.
Garibaldi, Skip
and
Guralnick, Robert M.
2022.
Generic Stabilizers for Simple Algebraic Groups.
Michigan Mathematical Journal,
Vol. 72,
Issue. none,
Scavia, Federico
2023.
STEENROD OPERATIONS ON THE DE RHAM COHOMOLOGY OF ALGEBRAIC STACKS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 2,
p.
493.
Kubrak, Dimitry
and
Scavia, Federico
2025.
Eilenberg-Moore spectral sequence and Hodge cohomology of classifying stacks.
Journal of Algebraic Geometry,
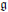 over an arbitrary base scheme S, we consider the quotient of
over an arbitrary base scheme S, we consider the quotient of 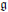 by the adjoint action of G. We study in detail the structure of
by the adjoint action of G. We study in detail the structure of 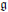 over S. Given a maximal torus T with Lie algebra
over S. Given a maximal torus T with Lie algebra  and associated Weyl group W, we show that the Chevalley morphism π :
and associated Weyl group W, we show that the Chevalley morphism π :  /W →
/W → 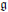 /G is an isomorphism except for the group Sp2n over a base with 2-torsion. In this case this morphism is only dominant and we compute it explicitly. We compute the adjoint quotient in some other classical cases, yielding examples where the formation of the quotient
/G is an isomorphism except for the group Sp2n over a base with 2-torsion. In this case this morphism is only dominant and we compute it explicitly. We compute the adjoint quotient in some other classical cases, yielding examples where the formation of the quotient 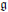 →
→ 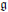 /G commutes, or does not commute, with base change on S.
/G commutes, or does not commute, with base change on S.