Article contents
Nearly ordinary Galois deformations over arbitrary number fields
Published online by Cambridge University Press: 04 April 2008
Abstract
Let K be an arbitrary number field, and let ρ : Gal(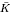 /K) → GL2(E) be a nearly ordinary irreducible geometric Galois representation. In this paper, we study the nearly ordinary deformations of ρ. When K is totally real and ρ is modular, results of Hida imply that the nearly ordinary deformation space associated to ρ contains a Zariski dense set of points corresponding to ‘automorphic’ Galois representations. We conjecture that if K is not totally real, then this is never the case, except in three exceptional cases, corresponding to: (1) ‘base change’, (2) ‘CM’ forms, and (3) ‘even’ representations. The latter case conjecturally can only occur if the image of ρ is finite. Our results come in two flavours. First, we prove a general result for Artin representations, conditional on a strengthening of the Leopoldt Conjecture. Second, when K is an imaginary quadratic field, we prove an unconditional result that implies the existence of ‘many’ positive-dimensional components (of certain deformation spaces) that do not contain infinitely many classical points. Also included are some speculative remarks about ‘p-adic functoriality’, as well as some remarks on how our methods should apply to n-dimensional representations of Gal(
/K) → GL2(E) be a nearly ordinary irreducible geometric Galois representation. In this paper, we study the nearly ordinary deformations of ρ. When K is totally real and ρ is modular, results of Hida imply that the nearly ordinary deformation space associated to ρ contains a Zariski dense set of points corresponding to ‘automorphic’ Galois representations. We conjecture that if K is not totally real, then this is never the case, except in three exceptional cases, corresponding to: (1) ‘base change’, (2) ‘CM’ forms, and (3) ‘even’ representations. The latter case conjecturally can only occur if the image of ρ is finite. Our results come in two flavours. First, we prove a general result for Artin representations, conditional on a strengthening of the Leopoldt Conjecture. Second, when K is an imaginary quadratic field, we prove an unconditional result that implies the existence of ‘many’ positive-dimensional components (of certain deformation spaces) that do not contain infinitely many classical points. Also included are some speculative remarks about ‘p-adic functoriality’, as well as some remarks on how our methods should apply to n-dimensional representations of Gal( /ℚ) when n > 2.
/ℚ) when n > 2.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 8 , Issue 1 , January 2009 , pp. 99 - 177
- Copyright
- Copyright © Cambridge University Press 2008
References
- 28
- Cited by

