Article contents
LOCALLY ANALYTIC VECTORS AND OVERCONVERGENT 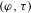 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
Published online by Cambridge University Press: 03 May 2019
Abstract
Let 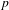 $p$ be a prime, let
$p$ be a prime, let 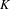 $K$ be a complete discrete valuation field of characteristic
$K$ be a complete discrete valuation field of characteristic  $0$ with a perfect residue field of characteristic
$0$ with a perfect residue field of characteristic 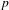 $p$, and let
$p$, and let 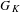 $G_{K}$ be the Galois group. Let
$G_{K}$ be the Galois group. Let  $\unicode[STIX]{x1D70B}$ be a fixed uniformizer of
$\unicode[STIX]{x1D70B}$ be a fixed uniformizer of 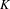 $K$, let
$K$, let 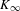 $K_{\infty }$ be the extension by adjoining to
$K_{\infty }$ be the extension by adjoining to 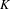 $K$ a system of compatible
$K$ a system of compatible 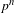 $p^{n}$th roots of
$p^{n}$th roots of  $\unicode[STIX]{x1D70B}$ for all
$\unicode[STIX]{x1D70B}$ for all  $n$, and let
$n$, and let  $L$ be the Galois closure of
$L$ be the Galois closure of 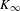 $K_{\infty }$. Using these field extensions, Caruso constructs the
$K_{\infty }$. Using these field extensions, Caruso constructs the 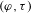 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules, which classify
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules, which classify 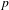 $p$-adic Galois representations of
$p$-adic Galois representations of 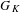 $G_{K}$. In this paper, we study locally analytic vectors in some period rings with respect to the
$G_{K}$. In this paper, we study locally analytic vectors in some period rings with respect to the 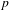 $p$-adic Lie group
$p$-adic Lie group 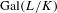 $\operatorname{Gal}(L/K)$, in the spirit of the work by Berger and Colmez. Using these locally analytic vectors, and using the classical overconvergent
$\operatorname{Gal}(L/K)$, in the spirit of the work by Berger and Colmez. Using these locally analytic vectors, and using the classical overconvergent 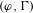 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules, we can establish the overconvergence property of the
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules, we can establish the overconvergence property of the 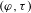 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules.
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-modules.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 137 - 185
- Copyright
- © Cambridge University Press 2019
References
- 3
- Cited by


