Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huybrechts, D.
and
Mauri, M.
2022.
Lagrangian Fibrations.
Milan Journal of Mathematics,
Vol. 90,
Issue. 2,
p.
459.
Debarre, Olivier
Huybrechts, Daniel
Macrì, Emanuele
and
Voisin, Claire
2023.
Computing Riemann–Roch polynomials and classifying hyper-Kähler fourfolds.
Journal of the American Mathematical Society,
Vol. 37,
Issue. 1,
p.
151.
Li, Yang
and
Tosatti, Valentino
2024.
Special Kähler geometry and holomorphic Lagrangian fibrations.
Comptes Rendus. Mathématique,
Vol. 362,
Issue. S1,
p.
171.
Ancona, Giuseppe
Cavicchi, Mattia
Laterveer, Robert
and
Saccà, Giulia
2025.
Relative and absolute Lefschetz standard conjectures for some Lagrangian fibrations.
Journal of the London Mathematical Society,
Vol. 111,
Issue. 4,
Liu, Yuchen
Liu, Zhiyu
and
Xu, Chenyang
2025.
Irreducible symplectic varieties with a large second Betti number.
Journal für die reine und angewandte Mathematik (Crelles Journal),

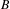
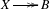 of a projective, irreducible symplectic fourfold
of a projective, irreducible symplectic fourfold