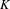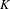Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schlichting, Marco
2019.
Symplectic and orthogonal K-groups of the integers.
Comptes Rendus. Mathématique,
Vol. 357,
Issue. 8,
p.
686.
Hudson, Thomas
Martirosian, Arthur
and
Xie, Heng
2022.
Witt groups of Spinor varieties.
Proceedings of the London Mathematical Society,
Vol. 125,
Issue. 5,
p.
1152.
Eberhardt, Jens Niklas
Lorscheid, Oliver
and
Young, Matthew B.
2022.
Algebraic $$K\!$$-theory and Grothendieck–Witt theory of monoid schemes.
Mathematische Zeitschrift,
Vol. 301,
Issue. 2,
p.
1407.
Voronetsky, E.
and
the author
2023.
Twisted forms of classical groups.
St. Petersburg Mathematical Journal,
Vol. 34,
Issue. 2,
p.
179.
Hebestreit, Fabian
Krause, Achim
and
Ramzi, Maxime
2024.
A note on quadratic forms.
Bulletin of the London Mathematical Society,
Vol. 56,
Issue. 5,
p.
1803.
Land, Markus
2024.
Gabber rigidity in hermitian K-theory.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 154,
Issue. 6,
p.
1842.
Hebestreit, Fabian
Lachmann, Andrea
and
Steimle, Wolfgang
2024.
The localisation theorem for the K-theory of stable ∞-categories.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 154,
Issue. 6,
p.
1749.