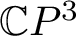Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brugallé, Erwan
López de Medrano, Lucía
and
Rau, Johannes
2024.
Combinatorial patchworking: Back from tropical geometry.
Transactions of the American Mathematical Society,