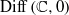Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rebelo, Julio C.
and
Reis, Helena
2017.
Discrete Orbits, Recurrence and Solvable Subgroups of $${{\mathrm{Diff}}\, ({{\mathbb {C}}}^2, 0)}$$ Diff ( C 2 , 0 ).
The Journal of Geometric Analysis,
Vol. 27,
Issue. 1,
p.
1.
Nakai, Isao
2024.
Handbook of Geometry and Topology of Singularities VI: Foliations.
p.
201.