Article contents
A BOUND FOR THE INDEX OF A QUADRATIC FORM AFTER SCALAR EXTENSION TO THE FUNCTION FIELD OF A QUADRIC
Published online by Cambridge University Press: 16 April 2018
Abstract
Let  $q$ be an anisotropic quadratic form defined over a general field
$q$ be an anisotropic quadratic form defined over a general field  $F$. In this article, we formulate a new upper bound for the isotropy index of
$F$. In this article, we formulate a new upper bound for the isotropy index of  $q$ after scalar extension to the function field of an arbitrary quadric. On the one hand, this bound offers a refinement of an important bound established in earlier work of Karpenko–Merkurjev and Totaro; on the other hand, it is a direct generalization of Karpenko’s theorem on the possible values of the first higher isotropy index. We prove its validity in two key cases: (i) the case where
$q$ after scalar extension to the function field of an arbitrary quadric. On the one hand, this bound offers a refinement of an important bound established in earlier work of Karpenko–Merkurjev and Totaro; on the other hand, it is a direct generalization of Karpenko’s theorem on the possible values of the first higher isotropy index. We prove its validity in two key cases: (i) the case where 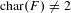 $\text{char}(F)\neq 2$, and (ii) the case where
$\text{char}(F)\neq 2$, and (ii) the case where 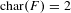 $\text{char}(F)=2$ and
$\text{char}(F)=2$ and  $q$ is quasilinear (i.e., diagonalizable). The two cases are treated separately using completely different approaches, the first being algebraic–geometric, and the second being purely algebraic.
$q$ is quasilinear (i.e., diagonalizable). The two cases are treated separately using completely different approaches, the first being algebraic–geometric, and the second being purely algebraic.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 421 - 450
- Copyright
- © Cambridge University Press 2018
References
- 3
- Cited by

