Article contents
APPLICATIONS OF INVOLUTIVE HEEGAARD FLOER HOMOLOGY
Published online by Cambridge University Press: 04 April 2019
Abstract
We use Heegaard Floer homology to define an invariant of homology cobordism. This invariant is isomorphic to a summand of the reduced Heegaard Floer homology of a rational homology sphere equipped with a spin structure and is analogous to Stoffregen’s connected Seiberg–Witten Floer homology. We use this invariant to study the structure of the homology cobordism group and, along the way, compute the involutive correction terms 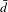 $\bar{d}$ and
$\bar{d}$ and 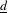 $\text{}\underline{d}$ for certain families of three-manifolds.
$\text{}\underline{d}$ for certain families of three-manifolds.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 187 - 224
- Copyright
- © Cambridge University Press 2019
Footnotes
The first author was partially supported by NSF grant DMS-1663778. The second author was partially supported by NSF grant DMS-1552285 and a Sloan Research Fellowship. The third author was partially supported by NSF grant DMS-1709702.
References
- 13
- Cited by


