Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shiffman, Bernard
and
Zelditch, Steve
2011.
Notions of Positivity and the Geometry of Polynomials.
p.
375.
Zelditch, S.
2012.
Large Deviations of Empirical Measures of Zeros on Riemann Surfaces.
International Mathematics Research Notices,
Hanin, Boris
2015.
Correlations and Pairing between Zeros and Critical Points of Gaussian Random Polynomials.
International Mathematics Research Notices,
Vol. 2015,
Issue. 2,
p.
381.
Feng, Renjie
2016.
Conditional Expectations of Random Holomorphic Fields on Riemann Surfaces.
International Mathematics Research Notices,
p.
rnw152.
Ghosh, Subhroshekhar
and
Peres, Yuval
2017.
Rigidity and tolerance in point processes: Gaussian zeros and Ginibre eigenvalues.
Duke Mathematical Journal,
Vol. 166,
Issue. 10,
Sun, Jingzhou
2021.
Logarithmic Bergman Kernel and Conditional Expectation of Gaussian Holomorphic Fields.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 8,
p.
8520.

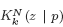 of zeros of a Gaussian system of random polynomials (and more generally, holomorphic sections), given that the polynomials or sections vanish at a point
of zeros of a Gaussian system of random polynomials (and more generally, holomorphic sections), given that the polynomials or sections vanish at a point 