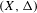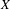Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nakamura, Yusuke
and
Witaszek, Jakub
2017.
On the base point free theorem and Mori dream spaces for log canonical threefolds over the algebraic closure of a finite field.
Mathematische Zeitschrift,
Vol. 287,
Issue. 3-4,
p.
1343.
Zhang, Lei
2017.
A Note on Iitaka's Conjecture $C_{3,1}$ in Positive
Characteristics.
Taiwanese Journal of Mathematics,
Vol. 21,
Issue. 3,
Birkar, Caucher
and
Waldron, Joe
2017.
Existence of Mori fibre spaces for 3-folds in char p.
Advances in Mathematics,
Vol. 313,
Issue. ,
p.
62.
Karzhemanov, Ilya
2017.
RETRACTED ARTICLE: Some pathologies of Fano manifolds in positive characteristic.
manuscripta mathematica,
Vol. 153,
Issue. 3-4,
p.
645.
Lehmann, Brian
2017.
Surveys on Recent Developments in Algebraic Geometry.
Vol. 95,
Issue. ,
p.
1.
BIRKAR, CAUCHER
CHEN, YIFEI
and
ZHANG, LEI
2018.
IITAKA CONJECTURE FOR 3-FOLDS OVER FINITE FIELDS.
Nagoya Mathematical Journal,
Vol. 229,
Issue. ,
p.
21.
Chiecchio, Alberto
Enescu, Florian
Miller, Lance Edward
and
Schwede, Karl
2018.
TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 17,
Issue. 1,
p.
171.
Zhang, Lei
2019.
Subadditivity of Kodaira dimensions for fibrations of three-folds in positive characteristics.
Advances in Mathematics,
Vol. 354,
Issue. ,
p.
106741.
Xu, Chenyang
and
Zhang, Lei
2019.
Nonvanishing for 3-folds in characteristic p>5.
Duke Mathematical Journal,
Vol. 168,
Issue. 7,
Zhang, Lei
2019.
Abundance for non‐uniruled 3‐folds with non‐trivial Albanese maps in positive characteristics.
Journal of the London Mathematical Society,
Vol. 99,
Issue. 2,
p.
332.
Sengupta, Akash Kumar
2021.
Manin’s conjecture and the Fujita invariant of
finite covers.
Algebra & Number Theory,
Vol. 15,
Issue. 8,
p.
2071.
Bhatt, Bhargav
Ma, Linquan
Patakfalvi, Zsolt
Schwede, Karl
Tucker, Kevin
Waldron, Joe
and
Witaszek, Jakub
2023.
Globally $\pmb{+}$-regular varieties and the minimal model program for threefolds in mixed characteristic.
Publications mathématiques de l'IHÉS,
Vol. 138,
Issue. 1,
p.
69.