Article contents
GENERALISED DIVISOR SUMS OF BINARY FORMS OVER NUMBER FIELDS
Published online by Cambridge University Press: 16 November 2017
Abstract
Estimating averages of Dirichlet convolutions 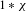 $1\ast \unicode[STIX]{x1D712}$, for some real Dirichlet character
$1\ast \unicode[STIX]{x1D712}$, for some real Dirichlet character  $\unicode[STIX]{x1D712}$ of fixed modulus, over the sparse set of values of binary forms defined over
$\unicode[STIX]{x1D712}$ of fixed modulus, over the sparse set of values of binary forms defined over  $\mathbb{Z}$ has been the focus of extensive investigations in recent years, with spectacular applications to Manin’s conjecture for Châtelet surfaces. We introduce a far-reaching generalisation of this problem, in particular replacing
$\mathbb{Z}$ has been the focus of extensive investigations in recent years, with spectacular applications to Manin’s conjecture for Châtelet surfaces. We introduce a far-reaching generalisation of this problem, in particular replacing  $\unicode[STIX]{x1D712}$ by Jacobi symbols with both arguments having varying size, possibly tending to infinity. The main results of this paper provide asymptotic estimates and lower bounds of the expected order of magnitude for the corresponding averages. All of this is performed over arbitrary number fields by adapting a technique of Daniel specific to
$\unicode[STIX]{x1D712}$ by Jacobi symbols with both arguments having varying size, possibly tending to infinity. The main results of this paper provide asymptotic estimates and lower bounds of the expected order of magnitude for the corresponding averages. All of this is performed over arbitrary number fields by adapting a technique of Daniel specific to 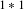 $1\ast 1$. This is the first time that divisor sums over values of binary forms are asymptotically evaluated over any number field other than
$1\ast 1$. This is the first time that divisor sums over values of binary forms are asymptotically evaluated over any number field other than 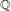 $\mathbb{Q}$. Our work is a key step in the proof, given in subsequent work, of the lower bound predicted by Manin’s conjecture for all del Pezzo surfaces over all number fields, under mild assumptions on the Picard number.
$\mathbb{Q}$. Our work is a key step in the proof, given in subsequent work, of the lower bound predicted by Manin’s conjecture for all del Pezzo surfaces over all number fields, under mild assumptions on the Picard number.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 1 , January 2020 , pp. 137 - 173
- Copyright
- © Cambridge University Press 2017
References
- 2
- Cited by

