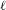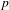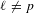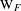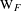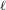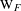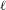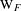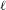Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kurinczuk, Robert
and
Matringe, Nadir
2020.
A characterization of the relation between two $\ell $-modular correspondences.
Comptes Rendus. Mathématique,
Vol. 358,
Issue. 2,
p.
201.
MOSS, GILBERT
2021.
CHARACTERIZING THE MOD- LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS.
Nagoya Mathematical Journal,
Vol. 244,
Issue. ,
p.
119.
Cui, Peiyi
Lanard, Thomas
and
Lu, Hengfei
2024.
Modulo ℓ distinction problems.
Compositio Mathematica,
Vol. 160,
Issue. 10,
p.
2285.
Nadimpalli, Santosh
and
Dhar, Sabyasachi
2024.
Tate Cohomology of Whittaker Lattices and Base Change of Generic Representations of GLn
.
International Mathematics Research Notices,
Vol. 2024,
Issue. 19,
p.
12761.