Article contents
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
Part of:
Complex dynamical systems
Special aspects of infinite or finite groups
Smooth dynamical systems: general theory
Holomorphic mappings and correspondences
Linear algebraic groups and related topics
Published online by Cambridge University Press: 22 January 2021
Abstract
We say that a group G of local (maybe formal) biholomorphisms satisfies the uniform intersection property if the intersection multiplicity 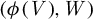 $(\phi (V), W)$ takes only finitely many values as a function of G for any choice of analytic sets V and W of complementary dimension. In dimension
$(\phi (V), W)$ takes only finitely many values as a function of G for any choice of analytic sets V and W of complementary dimension. In dimension 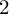 $2$ we show that G satisfies the uniform intersection property if and only if it is finitely determined – that is, if there exists a natural number k such that different elements of G have different Taylor expansions of degree k at the origin. We also prove that G is finitely determined if and only if the action of G on the space of germs of analytic curves has discrete orbits.
$2$ we show that G satisfies the uniform intersection property if and only if it is finitely determined – that is, if there exists a natural number k such that different elements of G have different Taylor expansions of degree k at the origin. We also prove that G is finitely determined if and only if the action of G on the space of germs of analytic curves has discrete orbits.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1677 - 1700
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
Arnold, V. I., Dynamics of complexity of intersections, Bol. Soc. Bras. Mat., Nova Sér., 21(1) (1990), 1–10.CrossRefGoogle Scholar
Arnold, V. I., Dynamics of intersections, in Analysis, et Cetera, pp. 77–84 (Academic Press, Boston, MA, 1990).CrossRefGoogle Scholar
Arnold, V. I., ed., Arnold’s Problems (Springer,
Berlin, 2004). Translated and revised edition of the 2000 Russian original.Google Scholar
Arnold, V. I., Bounds for Milnor numbers of intersections in holomorphic dynamical systems, in Topological Methods in Modern Mathematics: Proceedings of a Symposium in Honor of John Milnor’s Sixtieth Birthday, Held at the State University of New York at Stony Brook
, USA, June 14-June 21, 1991, pp. 379–390 (Publish or Perish, Inc.,
Houston, TX, 1993).Google Scholar
Baouendi, M. S., Preiss Rothschild, L., Winkelmann, J. and Zaitsev, D., Lie group structures on groups of diffeomorphisms and applications to CR manifolds, Ann. Inst. Fourier (Grenoble), 54(5) (2004), 1279–1303, 2004.Google Scholar
Binyamini, G., Finiteness properties of formal Lie group actions, Transform. Groups, 20(4) (2015), 939–952.Google Scholar
Borel, A.,
Linear Algebraic Groups
, 2nd ed., Graduate Texts in Mathematics no. 126, (Springer-Verlag,
New York, 1991.Google Scholar
Cerveau, D. and Mattei, J.-F., Formes intégrables holomorphes singulières, Astèrisque, 97:(1982).Google Scholar
Écalle, J., Théorie itérative: introduction à la théorie des invariants holomorphes, J.Math. Pures Appl. (9) 54 (1975), 183–258.Google Scholar
Favre, C. and Jonsson, M.,
The Valuative Tree
Lecture Notes in Mathematics no. 1853 (Springer-Verlag,
Berlin, 2004).Google Scholar
Ilyashenko, Y. and Yakovenko, S., Lectures on Analytic Differential Equations Graduate Studies in Mathematics no. 86 (American Mathematical Society,
Providence, RI, 2008).Google Scholar
Levy, A., Basic Set Theory (Dover Publications,
Mineola, NY, 2002). Reprint of the 1979 original.Google Scholar
Martelo, M. and Ribón, J., Derived length of solvable groups of local diffeomorphisms, Math. Ann. 358(3) (2014), 701–728.CrossRefGoogle Scholar
Martinet, J. and Ramis, J.-P., Classification analytique des équations differentielles non linéaires résonnantes du premier ordre, Ann. Sci. ÈEc. Norm. Supèr. (4), 4(16) (1983), 571–621.Google Scholar
Mattei, J. -F. and Moussu, R., Holonomie et intégrales premières, Ann. Sci. Èc. Norm. Supèr. (4), 13(4) (1908), 469–523.CrossRefGoogle Scholar
Ribón, J., Finite dimensional groups of local diffeomorphisms, Israel J.Math. 227(1) (2018), 289–329.Google Scholar
Ribón, J., The solvable length of groups of local diffeomorphisms, J.Reine Angew. Math. 752 (2019), 105–139.CrossRefGoogle Scholar
Seigal, A. L. and Yakovenko, S., Local dynamics of intersections: V. I. Arnold’s theorem revisited, Israel J.Math. 201(2) (2014), 813–833.CrossRefGoogle Scholar
Shastri, A. R., Elements of Differential Topology (CRC Press,
Boca Raton, FL, 2011). With a foreword by F. T. Farrell.CrossRefGoogle Scholar
Shub, M. and Sullivan, D., A remark on the Lefschetz fixed point formula for differentiable maps, Topology 13 (1974), 189–191.Google Scholar
Skolem, T., Ein Verfahren zur Behandlung gewisser exponentialer Gleichungen und diophantischer Gleichungen, in 8th Scand. Math. Congr., Stockholm, 1934, pp. 163–188 (Håkan Ohlssons Boktryckeri, Lund, 1935).Google Scholar
Wall, C. T. C., Singular Points of Plane Curves, London Mathematical Society Student Texts no. 63 (Cambridge University Press, 2004).Google Scholar
- 1
- Cited by


