Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
BORODULIN–NADZIEJA, PIOTR
FARKAS, BARNABÁS
and
PLEBANEK, GRZEGORZ
2015.
REPRESENTATIONS OF IDEALS IN POLISH GROUPS AND IN BANACH SPACES.
The Journal of Symbolic Logic,
Vol. 80,
Issue. 4,
p.
1268.
GARTSIDE, PAUL
and
MAMATELASHVILI, ANA
2016.
THE TUKEY ORDER ON COMPACT SUBSETS OF SEPARABLE METRIC SPACES.
The Journal of Symbolic Logic,
Vol. 81,
Issue. 1,
p.
181.
Drewnowski, Lech
and
Labuda, Iwo
2017.
Ideals of subseries convergence and F-spaces.
Archiv der Mathematik,
Vol. 108,
Issue. 1,
p.
55.
Gartside, Paul
and
Mamatelashvili, Ana
2018.
The Tukey Order and Subsets of ω 1.
Order,
Vol. 35,
Issue. 1,
p.
139.
HE, JIALIANG
HRUŠÁK, MICHAEL
ROJAS-REBOLLEDO, DIEGO
and
SOLECKI, SŁAWOMIR
2021.
TUKEY ORDER AMONG IDEALS.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 2,
p.
855.
KWELA, ADAM
and
LEONETTI, PAOLO
2022.
DENSITY-LIKE AND GENERALIZED DENSITY IDEALS.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 1,
p.
228.
FARKAS, BARNABÁS
and
ZDOMSKYY, LYUBOMYR
2022.
WAYS OF DESTRUCTION.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 3,
p.
938.
Kuzeljevic, Borisa
and
Todorcevic, Stevo
2023.
Cofinal types on ω2.
Mathematical Logic Quarterly,
Vol. 69,
Issue. 1,
p.
92.
Beros, Konstantinos A.
and
Larson, Paul B.
2024.
Maximal Tukey types, P-ideals and the weak Rudin–Keisler order.
Archive for Mathematical Logic,
Vol. 63,
Issue. 3-4,
p.
325.
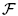 of clopen subsets of 2ℕ with the property that for each nowhere-dense subset of 2ℕ there is a set in
of clopen subsets of 2ℕ with the property that for each nowhere-dense subset of 2ℕ there is a set in 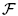 not intersecting it. We call such families avoiding.
not intersecting it. We call such families avoiding.