Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mosić, Dijana
Stanimirović, Predrag S.
and
Katsikis, Vasilios N.
2020.
Solvability of some constrained matrix approximation problems using core-EP inverses.
Computational and Applied Mathematics,
Vol. 39,
Issue. 4,
Mosić, Dijana
Dolinar, Gregor
and
Marovt, Janko
2021.
EP-quasinilpotent decomposition and its generalizations.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 4,
Mosić, Dijana
Kyrchei, Ivan I.
and
Stanimirović, Predrag S.
2021.
Representations and properties for the MPCEP inverse.
Journal of Applied Mathematics and Computing,
Vol. 67,
Issue. 1-2,
p.
101.
Mosić, Dijana
2022.
Weighted G-Outer Inverse of Banach Spaces Operators.
Numerical Functional Analysis and Optimization,
Vol. 43,
Issue. 5,
p.
558.
Kyrchei, Ivan I.
Mosić, Dijana
and
Stanimirović, Predrag S.
2022.
Representations of Quaternion W-MPCEP, W-CEPMP and W-MPCEPMP Inverses.
Advances in Applied Clifford Algebras,
Vol. 32,
Issue. 3,
Stanimirović, Predrag S.
Mosić, Dijana
and
Wei, Yimin
2022.
Generalizations of composite inverses with certain image and/or kernel.
Applied Mathematics and Computation,
Vol. 428,
Issue. ,
p.
127155.
Xu, Sanzhang
Wang, Dingguo
and
Benítez, Julio
2023.
New characterizations for the weighted (b, c)-inverse in rings and their applications.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 3,
Sitha, Bibekananda
Sahoo, Jajati Keshari
Behera, Ratikanta
Stanimirović, Predrag S.
and
Stupina, Alena A.
2023.
Generalized core-EP inverse for square matrices.
Computational and Applied Mathematics,
Vol. 42,
Issue. 8,
Kyrchei, Ivan I.
Mosić, Dijana
and
Stanimirović, Predrag S.
2023.
W-MPCEP–N-CEPMP-solutions to quaternion matrix equations with constrains.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 4,
Mosić, Dijana
and
Marovt, Janko
2024.
Weighted MP weak group inverse.
Analele Universitatii "Ovidius" Constanta - Seria Matematica,
Vol. 32,
Issue. 1,
p.
221.
Chen, Huanyin
and
Abdolyousefi, Marjan
2024.
Generalized weighted core inverse in Banach *-algebras.
Filomat,
Vol. 38,
Issue. 11,
p.
3691.
Jia, Boting
2024.
Similarity and approximation of EP operators.
Journal of Mathematical Analysis and Applications,
Vol. 531,
Issue. 1,
p.
127786.
Stanimirovic, Olivera
and
Mosic, Dijana
2025.
New properties of the core-EP pre-order.
Filomat,
Vol. 39,
Issue. 3,
p.
743.
Chen, Huanyin
and
Sheibani Abdolyousefi, Marjan
2025.
Weighted generalized group inverse in Banach *-algebras.
Filomat,
Vol. 39,
Issue. 2,
p.
483.
Mosić, Dijana
Dolinar, Gregor
Kuzma, Bojan
and
Marovt, Janko
2025.
Core–EP orthogonal operators.
Linear and Multilinear Algebra,
Vol. 73,
Issue. 10,
p.
2287.
Mosić, Dijana
2025.
Generalized MPD and DMP Inverses.
Numerical Functional Analysis and Optimization,
Vol. 46,
Issue. 2,
p.
89.
Stanimirović, Olivera
and
Mosić, Dijana
2025.
One-sided core–EP orthogonal operators.
Linear and Multilinear Algebra,
Vol. 73,
Issue. 13,
p.
2917.
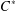 $C^{\ast }$-ALGEBRA
$C^{\ast }$-ALGEBRA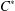 $C^{\ast }$-algebra. Some properties of the weighted core–EP inverse and weighted core–EP pre-orders are generalized and some new ones are proved. Using the weighted element, the weighted core–EP pre-order, the minus partial order and the star partial order of certain elements, new weighted pre-orders are presented on the set of all
$C^{\ast }$-algebra. Some properties of the weighted core–EP inverse and weighted core–EP pre-orders are generalized and some new ones are proved. Using the weighted element, the weighted core–EP pre-order, the minus partial order and the star partial order of certain elements, new weighted pre-orders are presented on the set of all 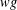 $wg$-Drazin invertible elements of a
$wg$-Drazin invertible elements of a 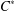 $C^{\ast }$-algebra. Applying these results, we introduce and characterize new partial orders which extend the core–EP pre-order to a partial order.
$C^{\ast }$-algebra. Applying these results, we introduce and characterize new partial orders which extend the core–EP pre-order to a partial order.

