Hostname: page-component-7f64f4797f-p4db6 Total loading time: 0 Render date: 2025-11-11T19:17:29.805Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAK POTENTIAL CONDITIONS FOR SCHRÖDINGER EQUATIONS WITH CRITICAL NONLINEARITIES

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  28 October 2015

X. H. TANG  and
SITONG CHEN
X. H. TANG*
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, PR China email tangxh@csu.edu.cn
SITONG CHEN
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, PR China email mathsitonchen@163.com
*
✉mathsitonchen@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove the existence of nontrivial solutions to the following Schrödinger equation with critical Sobolev exponent: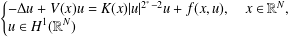

$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}-{\rm\Delta}u+V(x)u=K(x)|u|^{2^{\ast }-2}u+f(x,u),\quad x\in \mathbb{R}^{N},\\ u\in H^{1}(\mathbb{R}^{N})\end{array}\right.\end{eqnarray}$$
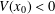under assumptions that (i) $V(x_{0})<0$ for some 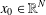$x_{0}\in \mathbb{R}^{N}$ and (ii) there exists 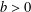$b>0$ such that the set 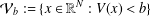${\mathcal{V}}_{b}:=\{x\in \mathbb{R}^{N}:V(x)<b\}$ has finite measure, in addition to some common assumptions on 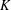$K$ and 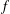$f$, where 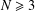$N\geq 3$, 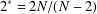$2^{\ast }=2N/(N-2)$.

Keywords

Schrödinger equationcritical Sobolev exponentweak potential conditions

MSC classification

Primary: 35J10: Schrödinger operator
Secondary: 35J20: Variational methods for second-order elliptic equations

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 2 , April 2016 , pp. 272 - 288
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bartsch, T., Pankov, A. and Wang, Z. Q., ‘Nonlinear Schrödinger equations with steep potential well’, Commun. Contemp. Math. 3 (2001), 549–569.Google Scholar
Bartsch, T. and Wang, Z.-Q., ‘Existence and multiplicity results for some superlinear elliptic problems on ℝN’, Comm. Partial Differential Equations 20 (1995), 1725–1741.Google Scholar
Bartsch, T., Wang, Z.-Q. and Willem, M., ‘The Dirichlet problem for superlinear elliptic equations’, in: Handbook of Differential Equations – Stationary Partial Differential Equations, Vol. 2 (eds. Chipot, M. and Quittner, P.) (Elsevier, Amsterdam, 2005), Ch. 1, 1–55.Google Scholar
Benci, V. and Cerami, G., ‘Existence of positive solutions of the equation −△u + a (x)u = u (N+2)∕(N−2) in ℝN’, J. Funct. Anal. 88(1) (1990), 90–117.Google Scholar
Brezis, H. and Nirenberg, L., ‘Positive solutions of nonlinear elliptic equations involving critical exponents’, Comm. Pure Appl. Math. 36 (1983), 437–477.Google Scholar
Capozzi, A., Fortunato, D. and Palmieri, G., ‘An existence result for nonlinear elliptic problems involving critical Sobolev exponent’, Ann. Inst. H. Poincaré Anal. Non Linéaire 2 (1985), 463–470.CrossRefGoogle Scholar
Chabrowski, J. and Szulkin, A., ‘On a semilinear Schrödinger equation with critical Sobolev exponent’, Proc. Amer. Math. Soc. 130 (2002), 85–93.CrossRefGoogle Scholar
Chabrowski, J. and Yang, J., ‘Existence theorems for the Schrödinger equation involving a critical Sobolev exponent’, Z. Angew. Math. Phys. 49 (1998), 276–293.Google Scholar
Chen, W., Wei, J. and Yan, S., ‘Infinitely many solutions for the Schrödinger equations in ℝN with critical growth’, J. Differential Equations 252 (2012), 2425–2447.CrossRefGoogle Scholar
Edmunds, D. E. and Evans, W. D., Spectral Theory and Differential Operators (Clarendon, Oxford, 1987).Google Scholar
Gidas, B., Ni, W. M. and Nirenberg, L., ‘Symmetry of positive solutions of nonlinear elliptic equations in ℝN’, Adv. Math. Suppl. Stud. A 7 (1981), 209–243.Google Scholar
Lin, X. and Tang, X. H., ‘Existence of infinitely many solutions for p-Laplacian equations in ℝN’, Nonlinear Anal. 92 (2013), 72–81.Google Scholar
Rabinowitz, P. H., ‘On a class of nonlinear Schröinger equations’, Z. Angew. Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
Simon, B., ‘Schrödinger semigroups’, Bull. Amer. Math. Soc. (N.S.) 7 (1982), 447–526.Google Scholar
Sirakov, B., ‘Existence and multiplicity of solutions of semilinear elliptic equations in ℝN’, Calc. Var. Partial Differ. Equ. 11 (2000), 119–142.CrossRefGoogle Scholar
Sun, J. and Wang, Z., Spectral Analysis for Linear Operators (Science Press, Beijing, 2005) (in Chinese).Google Scholar
Tang, X. H., ‘Infinitely many solutions for semilinear Schrödinger equations with sign-changing potential and nonlinearity’, J. Math. Anal. Appl. 401 (2013), 407–415.CrossRefGoogle Scholar
Tang, X. H., ‘New super-quadratic conditions on ground state solutions for superlinear Schrödinger equation’, Adv. Nonlinear Stud. 14 (2014), 361–373.CrossRefGoogle Scholar
Tang, X. H., ‘Non-Nehari manifold method for asymptotically linear Schrödinger equation’, J. Aust. Math. Soc. 98 (2015), 104–116.Google Scholar
Tang, X. H., ‘Non-Nehari manifold method for asymptotically periodic Schrödinger equations’, Sci. China Math. 58 (2015), 715–728.CrossRefGoogle Scholar
Willem, M., Minimax Theorems (Birkhäuser, Boston, MA, 1996).CrossRefGoogle Scholar
Zhang, Q. and Xu, B., ‘Multiplicity of solutions for a class of semilinear Schrödinger equations with sign-changing potential’, J. Math. Anal. Appl. 377 (2011), 834–840.Google Scholar