Article contents
VARIETIES OF LEFT RESTRICTION SEMIGROUPS
Published online by Cambridge University Press: 29 January 2018
Abstract
Left restriction semigroups are the unary semigroups that abstractly characterize semigroups of partial maps on a set, where the unary operation associates to a map the identity element on its domain. They may be defined by a simple set of identities and the author initiated a study of the lattice of varieties of such semigroups, in parallel with the study of the lattice of varieties of two-sided restriction semigroups. In this work we study the subvariety 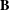 $\mathbf{B}$ generated by Brandt semigroups and the subvarieties generated by the five-element Brandt inverse semigroup
$\mathbf{B}$ generated by Brandt semigroups and the subvarieties generated by the five-element Brandt inverse semigroup 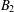 $B_{2}$, its four-element restriction subsemigroup
$B_{2}$, its four-element restriction subsemigroup 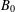 $B_{0}$ and its three-element left restriction subsemigroup
$B_{0}$ and its three-element left restriction subsemigroup 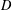 $D$. These have already been studied in the ‘plain’ semigroup context, in the inverse semigroup context (in the first two instances) and in the two-sided restriction semigroup context (in all but the last instance). The author has previously shown that in the last of these contexts, the behavior is pathological: ‘almost all’ finite restriction semigroups are inherently nonfinitely based. Here we show that this is not the case for left restriction semigroups, by exhibiting identities for the above varieties and for their joins with monoids (the analog of groups in this context). We do so by structural means involving subdirect decompositions into certain primitive semigroups. We also show that each identity has a simple structural interpretation.
$D$. These have already been studied in the ‘plain’ semigroup context, in the inverse semigroup context (in the first two instances) and in the two-sided restriction semigroup context (in all but the last instance). The author has previously shown that in the last of these contexts, the behavior is pathological: ‘almost all’ finite restriction semigroups are inherently nonfinitely based. Here we show that this is not the case for left restriction semigroups, by exhibiting identities for the above varieties and for their joins with monoids (the analog of groups in this context). We do so by structural means involving subdirect decompositions into certain primitive semigroups. We also show that each identity has a simple structural interpretation.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 105 , Issue 2 , October 2018 , pp. 173 - 200
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

