Article contents
Varieties of distributive lattices with unary operations I
Published online by Cambridge University Press: 09 April 2009
Abstract
A unified study is undertaken of finitely generated varieties HSP (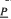 ) of distributive lattices with unary operations, extending work of Cornish. The generating algebra (
) of distributive lattices with unary operations, extending work of Cornish. The generating algebra (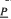 ) is assusmed to be of the form (P; ∧, ∨, 0, 1, {fμ}), where each fμ is an endomorphism or dual endomorphism of (P; ∧, ∨, 0, 1), and the Priestly dual of this lattice is an ordered semigroup N whose elements act by left multiplication to give the maps dual to the operations fμ. Duality theory is fully developed within this framework, into which fit many varieties arising in algebraic logic. Conditions on N are given for the natural and Priestley dualities for HSP (
) is assusmed to be of the form (P; ∧, ∨, 0, 1, {fμ}), where each fμ is an endomorphism or dual endomorphism of (P; ∧, ∨, 0, 1), and the Priestly dual of this lattice is an ordered semigroup N whose elements act by left multiplication to give the maps dual to the operations fμ. Duality theory is fully developed within this framework, into which fit many varieties arising in algebraic logic. Conditions on N are given for the natural and Priestley dualities for HSP (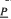 ) to be essentially the same, so that, inter alia, coproducts in HSP (
) to be essentially the same, so that, inter alia, coproducts in HSP (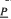 ) are enriched D-coproducts.
) are enriched D-coproducts.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1997
References
- 7
- Cited by

