Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Njåstad, Olav
1987.
Unique solvability of an extended Hamburger moment problem.
Journal of Mathematical Analysis and Applications,
Vol. 124,
Issue. 2,
p.
502.
Njastad, Olav
1988.
Orthogonal Polynomials and their Applications.
Vol. 1329,
Issue. ,
p.
300.
Jones, William B.
and
Thron, W.J.
1988.
Continued fractions in numerical analysis.
Applied Numerical Mathematics,
Vol. 4,
Issue. 2-4,
p.
143.
Njåstad, Olav
1988.
Solution of the strong hamburger moment problem by Laurent continued fractions.
Applied Numerical Mathematics,
Vol. 4,
Issue. 2-4,
p.
351.
González-Vera, Pablo
and
Njåstad, Olav
1990.
Convergence of two-point Padé approximants to series of Stieltjes.
Journal of Computational and Applied Mathematics,
Vol. 32,
Issue. 1-2,
p.
97.
Njåstad, Olav
1991.
A modified Schur algorithm and an extended Hamburger moment problem.
Transactions of the American Mathematical Society,
Vol. 327,
Issue. 1,
p.
283.
Ranga, A. Sri
1992.
The strong c-Symmetric distribution.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 53,
Issue. 2,
p.
261.
Merkes, E.P.
and
Wetzel, Marion
1992.
Backward Extensions and Strong Hamburger Moment Sequences.
Rocky Mountain Journal of Mathematics,
Vol. 22,
Issue. 1,
González-Concepción, C.
González-Vera, P.
and
Hendriksen, E.
1992.
Matrix orthogonal Laurent polynomials and two-point Padé approximants.
Numerical Algorithms,
Vol. 3,
Issue. 1,
p.
201.
Bultheel, A.
González-Vera, P.
Hendriksen, E.
and
Njåstad, O.
1993.
Moment problems and orthogonal functions.
Journal of Computational and Applied Mathematics,
Vol. 48,
Issue. 1-2,
p.
49.
Njåstad, Olav
1995.
Extremal solutions of the strong Stieltjes moment problem.
Journal of Computational and Applied Mathematics,
Vol. 65,
Issue. 1-3,
p.
309.
Njåstad, Olav
1998.
Nevanlinna matrices for the strong Stieltjes moment problem.
Journal of Computational and Applied Mathematics,
Vol. 99,
Issue. 1-2,
p.
311.
Jones, William B.
and
Njåstad, Olav
1999.
Orthogonal Laurent polynomials and strong moment theory: a survey.
Journal of Computational and Applied Mathematics,
Vol. 105,
Issue. 1-2,
p.
51.
Hendriksen, Erik
and
Nijhuis, Caspar
2000.
Laurent–Jacobi Matrices and the Strong Hamburger Moment Problem.
Acta Applicandae Mathematica,
Vol. 61,
Issue. 1-3,
p.
119.
Bultheel, Adhemar
Gonzalez-Vera, Pablo
Hendriksen, Erik
and
Njåstad, Olav
2001.
Special Functions 2000: Current Perspective and Future Directions.
p.
87.
Njåstad, O.
2003.
Nevanlinna Matrices for the Strong Hamburger Moment Problem.
Rocky Mountain Journal of Mathematics,
Vol. 33,
Issue. 2,
Díaz-Mendoza, C.
González-Vera, P.
and
Jiménez Paiz, M.
2005.
Orthogonal Laurent polynomials and two-point Padé approximants associated with Dawson's integral.
Journal of Computational and Applied Mathematics,
Vol. 179,
Issue. 1-2,
p.
195.
McLaughlin, K. T.-R.
Vartanian, A. H.
and
Zhou, X.
2008.
Asymptotics of Recurrence Relation Coefficients, Hankel Determinant Ratios, and Root Products Associated with Laurent Polynomials Orthogonal with Respect to Varying Exponential Weights.
Acta Applicandae Mathematicae,
Vol. 100,
Issue. 1,
p.
39.
McLaughlin, K. T.- R.
Vartanian, A. H.
and
Zhou, X.
2010.
Asymptotics of Laurent polynomials of even degree orthogonal with respect to varying exponential weights.
International Mathematics Research Papers,
Nailwal, Rajkamal
and
Zalar, Aljaž
2025.
The truncated univariate rational moment problem.
Linear Algebra and its Applications,
Vol. 708,
Issue. ,
p.
280.
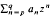 . By this means the authors and W. B. Jones (J. Math. Anal. Appl. 98 (1984), 528–554) solved the strong Hamburger moment problem, that is, given a double sequence
. By this means the authors and W. B. Jones (J. Math. Anal. Appl. 98 (1984), 528–554) solved the strong Hamburger moment problem, that is, given a double sequence 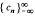 , to find a distribution function ψ(t), non-decreasing, with an infinitenumber of points of increase and bounded on −∞ < t < ∞, such that for all integers
, to find a distribution function ψ(t), non-decreasing, with an infinitenumber of points of increase and bounded on −∞ < t < ∞, such that for all integers 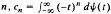 . In this article further menthods such as analogues of the Lioville-Ostrogradski formula and of the Christoffel-Darboux formula are developed to investigated When the moment porblem has a unique solution. This will be the case if and only if a sequence of nested disks associated with the sequence
. In this article further menthods such as analogues of the Lioville-Ostrogradski formula and of the Christoffel-Darboux formula are developed to investigated When the moment porblem has a unique solution. This will be the case if and only if a sequence of nested disks associated with the sequence 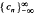 has only a point as its intersection (the so called limit point case).
has only a point as its intersection (the so called limit point case).
