No CrossRef data available.
Article contents
SYSTEMS OF ISLANDS WITH CONTINUOUS HEIGHT FUNCTIONS
Published online by Cambridge University Press: 01 May 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We investigate island systems with continuous height functions and strongly laminar systems which are laminar systems containing sets with disjoint boundaries. In the discrete case, we show that for a maximal rectangular system of islands 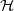 $ \mathcal{H} $ on an
$ \mathcal{H} $ on an 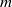 $m$ by
$m$ by  $n$ rectangular grid we have
$n$ rectangular grid we have 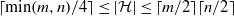 $\lceil \min (m, n)/ 4\rceil \leq \vert \mathcal{H} \vert \leq \lceil m/ 2\rceil \lceil n/ 2\rceil $. In the continuous case we show that under some conditions maximal strongly laminar systems
$\lceil \min (m, n)/ 4\rceil \leq \vert \mathcal{H} \vert \leq \lceil m/ 2\rceil \lceil n/ 2\rceil $. In the continuous case we show that under some conditions maximal strongly laminar systems 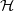 $ \mathcal{H} $ have cardinality
$ \mathcal{H} $ have cardinality 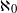 ${\aleph }_{0} $ or
${\aleph }_{0} $ or 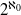 ${2}^{{\aleph }_{0} } $ and present examples with
${2}^{{\aleph }_{0} } $ and present examples with 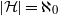 $\vert \mathcal{H} \vert = {\aleph }_{0} $.
$\vert \mathcal{H} \vert = {\aleph }_{0} $.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Baráth, J., Hajnal, P. and Horváth, E. K., ‘Elementary proof techniques for the maximum number of islands’, European J. Combin. 32 (2011), 276–281.CrossRefGoogle Scholar
Czédli, G., ‘The number of rectangular islands by means of distributive lattices’, European J. Combin. 30 (2009), 208–215.CrossRefGoogle Scholar
Czédli, G., Huhn, A. P. and Schmidt, E. T., ‘Weakly independent subsets in lattices’, Algebra Universalis 20 (1985), 194–196.CrossRefGoogle Scholar
Földes, S. and Singhi, N. M., ‘On instantaneous codes’, J. Comb. Inf. Syst. Sci. 31 (2006), 317–326.Google Scholar
Horváth, E. K., Horváth, G., Németh, Z. and Szabó, Cs., ‘The number of square islands on a rectangular sea’, Acta Sci. Math. (Szeged) 76 (2010), 35–48.CrossRefGoogle Scholar
Horváth, E. K., Németh, Z. and Pluhár, G., ‘The number of triangular islands on a triangular grid’, Period. Math. Hungar. 58 (2009), 25–34.CrossRefGoogle Scholar
Horváth, E. K., Šešelja, B. and Tepavčević, A., ‘Cut approach to islands in rectangular fuzzy relations’, Fuzzy Sets and Systems 161 (2010), 3114–3126.CrossRefGoogle Scholar
Lengvárszky, Zs., ‘The minimum cardinality of maximal systems of rectangular islands’, European J. Combin. 30 (2009), 216–219.CrossRefGoogle Scholar
Lengvárszky, Zs., ‘The size of maximal systems of square islands’, European J. Combin. 30 (2009), 889–892.CrossRefGoogle Scholar
Lengvárszky, Zs., ‘Notes on triangular islands’, Acta Sci. Math. (Szeged) 75 (2009), 369–376.Google Scholar
Lengvárszky, Zs. and Pach, P. P., ‘A note on systems of rectangular islands: the continuous case’, Acta Sci. Math. (Szeged) 77 (2011), 27–34.CrossRefGoogle Scholar
Máder, A. and Makay, G., ‘The maximum number of rectangular islands’, The Teaching of Math. 14 (2011), 31–44.Google Scholar
Pach, P. P., Pluhár, G., Pongrácz, A. and Szabó, Cs., ‘The possible number of islands on the sea’, J. Math. Anal. Appl. 375 (2011), 8–13.CrossRefGoogle Scholar
Pluhár, G., ‘The number of brick islands by means of distributive lattices’, Acta Sci. Math. (Szeged) 75 (2009), 3–11.Google Scholar
Thim, J., ‘Continuous nowhere differentiable functions’, Master’s Thesis, Luleå University of Technology, 2003.Google Scholar

