No CrossRef data available.
Article contents
Symplectic complex bundles over real algebraic four-folds
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let X be a compact affine real algebraic variety of dimension 4. We compute the Witt group of symplectic bilinear forms over the ring of regular functions from X to C. The Witt group is expressed in terms of some subgroups of the cohomology groups 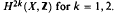 .
.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 47 , Issue 3 , December 1989 , pp. 430 - 437
- Copyright
- Copyright © Australian Mathematical Society 1989
References
[1]Barge, J. and Ojanguren, M., ‘Fibrés algébriques sur une surface réele,’ Comment. Math. Helv. 62 (1987), 616–629.CrossRefGoogle Scholar
[2]Bass, H., ‘Unitary algebraic K-theory,’ Algebraic K-Theory III, pp. 57–265 (Lecture Notes in Math., vol.343, Berlin, Heidelberg, New York, Springer 1973).Google Scholar
[3]Bochnak, J., Coste, M. and Roy, M.-F., Géométrie algébrique réele, (Ergebnisse Math. Grenzgeb., vol. 12, Springer, 1987).Google Scholar
[4]Bochnak, J., Buchner, M. and Kucharz, W., lsquo;Vector bundles over real algebraic varieties,’ to appear in K-Theory.Google Scholar
[5]Borel, A. and Haefliger, H., ‘La classe d'homologie fondamentale d'un espace analytique,’ Bull. Soc. Math. France 89 (1961), 461–513.CrossRefGoogle Scholar
[6]Buchner, M. and Kucharz, W., ‘Algebraic vector bundles over real algebraic varieties,’ Bull. Amer. Math. Soc. 17 (1987), 279–282.CrossRefGoogle Scholar
[7]Fulton, W., Intersection theory, (Ergebnisse Math. Grenzgeb., vol. 2, Springer, 1984).CrossRefGoogle Scholar
[10]Milnor, J. and Stasheff, J., Characteristic classes, (Princeton, Princeton University Press, 1974).CrossRefGoogle Scholar
[11]Ojanguren, M., Parimala, R. and Sridharan, R., ‘Symplectic bundles over affine varieties,’ Comment. Math. Helv. 61 (1986), 491–500.CrossRefGoogle Scholar
[12]Swan, R., ‘Vector bundles and projective modules,’ Trans. Amer. Math. Soc. 105 (1962), 264–277.CrossRefGoogle Scholar
[13]Swan, R., ‘Topological examples of projective modules,’ Trans. Amer. Math. Soc. 230 (1977), 201–234.CrossRefGoogle Scholar

