Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mantero, Anna Maria
and
Zappa, Anna
1987.
Irreducibility of the analytic continuation of the principal series of a free group.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 43,
Issue. 2,
p.
199.
Hashizume, Michihiko
1988.
Representations of Lie Groups, Kyoto, Hiroshima, 1986.
p.
395.
HIRAI, Takeshi
1990.
Some aspects in the theory of representations of discrete groups.
Japanese journal of mathematics. New series,
Vol. 16,
Issue. 2,
p.
197.
Kuhn, G.
and
Vershik, A.
2003.
Canonical Semigroups of States and Cocycles for the Group of Automorphisms of a Homogeneous Tree.
Algebras and Representation Theory,
Vol. 6,
Issue. 3,
p.
333.

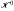 be the space of functions on the Poission boundary ω, of zero mean on ω. When
be the space of functions on the Poission boundary ω, of zero mean on ω. When 