Article contents
Some results on the asymptotic behavior of nonoscillatory solutions of differential equations with deviating arguments
Published online by Cambridge University Press: 09 April 2009
Abstract
This paper deals with some asymptotic properties of nonoscillatory solutions of a class of n-th order (n < 1) differential equations with deviationg arguments involving the so called n-th order r-derivative of the unknown function x defined by
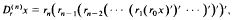
where ri (i = 0,1…n) are positive continous functions on [t0, ∞). The fundamental purpose of this paper is to find for any integer m, 0 < m < n – 1, a necessary and sufficient condition (depending on m) in order that three exists at least one (nonoscillatory) solution x so that the 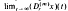 exists in R – {0} The results obtained extend some recent ones due to Philos (1978a) and they prove, in a general setting, the validity of a conjecture made by Kusano and Onose (1975).
exists in R – {0} The results obtained extend some recent ones due to Philos (1978a) and they prove, in a general setting, the validity of a conjecture made by Kusano and Onose (1975).
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1982
References
- 6
- Cited by

