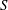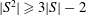Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Freiman, G.A.
Herzog, M.
Longobardi, P.
Maj, M.
and
Stanchescu, Y.V.
2014.
Direct and inverse problems in additive number theory and in non-abelian group theory.
European Journal of Combinatorics,
Vol. 40,
Issue. ,
p.
42.
Freiman, G.A.
Herzog, M.
Longobardi, P.
Maj, M.
and
Stanchescu, Y.V.
2015.
A small doubling structure theorem in a Baumslag–Solitar group.
European Journal of Combinatorics,
Vol. 44,
Issue. ,
p.
106.
Freiman, G.A.
Herzog, M.
Longobardi, P.
Maj, M.
Plagne, A.
Robinson, D.J.S.
and
Stanchescu, Y.V.
2016.
On the structure of subsets of an orderable group with some small doubling properties.
Journal of Algebra,
Vol. 445,
Issue. ,
p.
307.
Plagne, Alain
and
Tringali, Salvatore
2016.
Sums of Dilates in Ordered Groups.
Communications in Algebra,
Vol. 44,
Issue. 12,
p.
5223.
Freiman, Gregory A.
Herzog, Marcel
Longobardi, Patrizia
Maj, Mercede
and
Stanchescu, Yonutz V.
2018.
Small doubling in ordered nilpotent groups of class 2.
European Journal of Combinatorics,
Vol. 67,
Issue. ,
p.
87.
PANDEY, PREM PRAKASH
2018.
THE THEOREM FOR ORDERED GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 97,
Issue. 1,
p.
43.
Farrokhi Derakhshandeh Ghouchan, Mohammad
and
Jafari, S. H.
2018.
On the probability of being a deficient square group on 2-element subsets.
Communications in Algebra,
Vol. 46,
Issue. 3,
p.
1259.