No CrossRef data available.
Article contents
SIMPLICITY OF CROSSED PRODUCTS BY TWISTED PARTIAL ACTIONS
Published online by Cambridge University Press: 08 April 2019
Abstract
In this article, we consider a twisted partial action  $\unicode[STIX]{x1D6FC}$ of a group
$\unicode[STIX]{x1D6FC}$ of a group 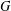 $G$ on an associative ring
$G$ on an associative ring 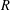 $R$ and its associated partial crossed product
$R$ and its associated partial crossed product 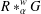 $R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$. We provide necessary and sufficient conditions for the commutativity of
$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$. We provide necessary and sufficient conditions for the commutativity of 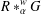 $R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$ when the twisted partial action
$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$ when the twisted partial action  $\unicode[STIX]{x1D6FC}$ is unital. Moreover, we study necessary and sufficient conditions for the simplicity of
$\unicode[STIX]{x1D6FC}$ is unital. Moreover, we study necessary and sufficient conditions for the simplicity of 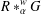 $R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$ in the following cases: (i)
$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$ in the following cases: (i) 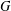 $G$ is abelian; (ii)
$G$ is abelian; (ii) 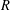 $R$ is maximal commutative in
$R$ is maximal commutative in 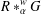 $R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$; (iii)
$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$; (iii) 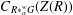 $C_{R\ast _{\unicode[STIX]{x1D6FC}}^{w}G}(Z(R))$ is simple; (iv)
$C_{R\ast _{\unicode[STIX]{x1D6FC}}^{w}G}(Z(R))$ is simple; (iv) 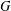 $G$ is hypercentral. When
$G$ is hypercentral. When 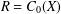 $R=C_{0}(X)$ is the algebra of continuous functions defined on a locally compact and Hausdorff space
$R=C_{0}(X)$ is the algebra of continuous functions defined on a locally compact and Hausdorff space 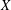 $X$, with complex values that vanish at infinity, and
$X$, with complex values that vanish at infinity, and 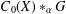 $C_{0}(X)\ast _{\unicode[STIX]{x1D6FC}}G$ is the associated partial skew group ring of a partial action
$C_{0}(X)\ast _{\unicode[STIX]{x1D6FC}}G$ is the associated partial skew group ring of a partial action  $\unicode[STIX]{x1D6FC}$ of a topological group
$\unicode[STIX]{x1D6FC}$ of a topological group 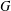 $G$ on
$G$ on 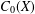 $C_{0}(X)$, we study the simplicity of
$C_{0}(X)$, we study the simplicity of 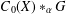 $C_{0}(X)\ast _{\unicode[STIX]{x1D6FC}}G$ by using topological properties of
$C_{0}(X)\ast _{\unicode[STIX]{x1D6FC}}G$ by using topological properties of 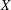 $X$ and the results about the simplicity of
$X$ and the results about the simplicity of 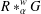 $R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$.
$R\ast _{\unicode[STIX]{x1D6FC}}^{w}G$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.

