Article contents
SHORT INTERVALS ASYMPTOTIC FORMULAE FOR BINARY PROBLEMS WITH PRIME POWERS, II
Published online by Cambridge University Press: 08 April 2019
Abstract
We improve some results in our paper [A. Languasco and A. Zaccagnini, ‘Short intervals asymptotic formulae for binary problems with prime powers’, J. Théor. Nombres Bordeaux 30 (2018) 609–635] about the asymptotic formulae in short intervals for the average number of representations of integers of the forms 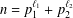 $n=p_{1}^{\ell _{1}}+p_{2}^{\ell _{2}}$ and
$n=p_{1}^{\ell _{1}}+p_{2}^{\ell _{2}}$ and 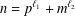 $n=p^{\ell _{1}}+m^{\ell _{2}}$, where
$n=p^{\ell _{1}}+m^{\ell _{2}}$, where 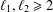 $\ell _{1},\ell _{2}\geq 2$ are fixed integers,
$\ell _{1},\ell _{2}\geq 2$ are fixed integers, 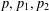 $p,p_{1},p_{2}$ are prime numbers and
$p,p_{1},p_{2}$ are prime numbers and  $m$ is an integer. We also remark that the techniques here used let us prove that a suitable asymptotic formula for the average number of representations of integers
$m$ is an integer. We also remark that the techniques here used let us prove that a suitable asymptotic formula for the average number of representations of integers 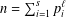 $n=\sum _{i=1}^{s}p_{i}^{\ell }$, where
$n=\sum _{i=1}^{s}p_{i}^{\ell }$, where  $s$,
$s$, 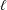 $\ell$ are two integers such that
$\ell$ are two integers such that 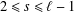 $2\leq s\leq \ell -1$,
$2\leq s\leq \ell -1$, 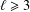 $\ell \geq 3$ and
$\ell \geq 3$ and 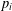 $p_{i}$,
$p_{i}$, 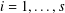 $i=1,\ldots ,s$, are prime numbers, holds in short intervals.
$i=1,\ldots ,s$, are prime numbers, holds in short intervals.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 109 , Issue 3 , December 2020 , pp. 351 - 370
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by I. Shparlinski
References
- 2
- Cited by


