Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dempwolff, Ulrich
2010.
On irreducible semilinear transformations.
Forum Mathematicum,
Vol. 22,
Issue. 6,
Dempwolff, Ulrich
2011.
Autotopism groups of cyclic semifield planes.
Journal of Algebraic Combinatorics,
Vol. 34,
Issue. 4,
p.
641.
2013.
Handbook of Finite Fields.
p.
777.
Lavrauw, Michel
2013.
Finite semifields and nonsingular tensors.
Designs, Codes and Cryptography,
Vol. 68,
Issue. 1-3,
p.
205.
Sheekey, John
2020.
New semifields and new MRD codes from skew polynomial rings.
Journal of the London Mathematical Society,
Vol. 101,
Issue. 1,
p.
432.
Göloğlu, Faruk
and
Kölsch, Lukas
2024.
Counting the number of non-isotopic Taniguchi semifields.
Designs, Codes and Cryptography,
Vol. 92,
Issue. 3,
p.
681.

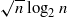 different nondesarguesian planes.
different nondesarguesian planes.