Article contents
Second-order strongly elliptic operators on Lie groups with Hölder continuous coefficients
Published online by Cambridge University Press: 09 April 2009
Abstract
Let G be a connected Lie group with Lie algebra g and a1, …, ad an algebraic basis of g. Further let Ai denote the generators of left translations, acting on the Lp-spaces Lp(G; dg) formed with left Haar measure dg, in the directions ai. We consider second-order operators 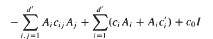 in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients cij and lower order coefficients ci, c′ii, c0 ∈ L∞ such that the matrix C= (cij) of principal coefficients satisfies the subellipticity condition
in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients cij and lower order coefficients ci, c′ii, c0 ∈ L∞ such that the matrix C= (cij) of principal coefficients satisfies the subellipticity condition 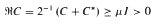 uniformly over G.
uniformly over G.
We discuss the hierarchy relating smoothness properties of the coefficients of H with smoothness of the kernel and smoothness of the domain of powers of H on the Lρ-spaces. Moreover, we present Gaussian type bounds for the kernel and its derivatives.
Similar theorems are proved for strongly elliptic operators 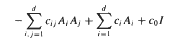 in non-divergence form for which the principal coefficients are at least once differentiable.
in non-divergence form for which the principal coefficients are at least once differentiable.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 63 , Issue 3 , December 1997 , pp. 297 - 363
- Copyright
- Copyright © Australian Mathematical Society 1997
References
- 4
- Cited by

