Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mohamed, Saad
Müller, Bruno J.
and
Singh, Surjeet
1985.
Quasi-dual-continuous modules.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 39,
Issue. 3,
p.
287.
Tuganbaev, A. A.
1999.
Skew-injective modules.
Journal of Mathematical Sciences,
Vol. 95,
Issue. 4,
p.
2328.

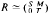 where
where 