No CrossRef data available.
Article contents
The ~ -representations of symmetric homogeneous algebras
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In 1947 I. E. Segal proved that to each non-degenerate ~ -representation R of L1 (= L1 (G) for a compact group G) with representation space , there corresponds a continuous unitary representation W of G, also with representation space , which satisfies
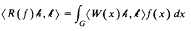
for each fL1 and hk. This was extended to Lp,1p < , in 1970 by E. Hewitt and K. A. Ross. We now generalize this result to any symmetric homogeneous convolution Banach alebra of pseudomeasures on G. Further we prove that the correspondence preserves irreduibility.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright Australian Mathematical Society 1986
References
1Edwards, R. E., Functional analysis, theory and applications (Holt, Rinehart and Winston, New York, 1965).Google Scholar
2Hewitt, E. and Ross, K. A., Abstract harmonic analysis, Vols. 1 and 2 (Springer-Verlag, Berlin, 1963 and 1970).Google Scholar
4Segal, I. E., The group algebra of a locally compact group, Trans. Amer. Math. Soc. 61 (1947), 69105.Google Scholar
5Ward, J. A., Characterization of homogeneous spaces and their norms, Pacific J. Math. 114 (1984), 481495.Google Scholar
6Ward, J. A., Closed ideals of homogeneous algebras, Monatsh. Math. 96 (1983), 317324.Google Scholar

