No CrossRef data available.
Article contents
Representations of minimally almost periodic groups
Published online by Cambridge University Press: 09 April 2009
Abstract
For any group G, we introduce the subset S(G) of elements g which are conjugate to 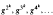 for some positive integer k. We show that, for any bounded representation π of G any g in S(G), either π(g) = 1 or the spectrum of π(g) is the full unit circle in C. As a corollary, S(G) is in the kernel of any homomorphism from G to the unitary group of a post-liminal C*-algebra with finite composition series.
for some positive integer k. We show that, for any bounded representation π of G any g in S(G), either π(g) = 1 or the spectrum of π(g) is the full unit circle in C. As a corollary, S(G) is in the kernel of any homomorphism from G to the unitary group of a post-liminal C*-algebra with finite composition series.
Next, for a topological group G, we consider the subset of elements approximately conjugate to 1, and we prove that it is contained in the kernel of any uniformly continuous bounded representation of G, and of any strongly continuous unitary representation in a finite von Neumann algebra.
We apply these results to prove triviality for a number of representations of isotropic simple algebraic groups defined over various fields.
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 41 , Issue 3 , December 1986 , pp. 366 - 375
- Copyright
- Copyright © Australian Mathematical Society 1986

