Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-11T09:09:32.654Z Has data issue: false hasContentIssue false
  • English
  • Français

THE REGULAR PART OF A SEMIGROUP OF LINEAR TRANSFORMATIONS WITH RESTRICTED RANGE

Part of: Semigroups

Published online by Cambridge University Press:  20 February 2017

WORACHEAD SOMMANEE  and
KRITSADA SANGKHANAN
WORACHEAD SOMMANEE
Affiliation:
Department of Mathematics and Statistics, Faculty of Science and Technology, Chiang Mai Rajabhat University, Chiang Mai 50300, Thailand email worachead_som@cmru.ac.th
KRITSADA SANGKHANAN*
Affiliation:
Department of Mathematics, Faculty of Science, Chiang Mai University, Chiang Mai 50200, Thailand email kritsada.s@cmu.ac.th
*
✉kritsada.s@cmu.ac.th
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 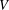$V$ be a vector space and let 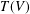$T(V)$ denote the semigroup (under composition) of all linear transformations from 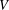$V$ into 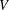$V$. For a fixed subspace 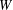$W$ of 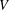$V$, let 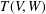$T(V,W)$ be the semigroup consisting of all linear transformations from 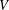$V$ into 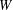$W$. In 2008, Sullivan [‘Semigroups of linear transformations with restricted range’, Bull. Aust. Math. Soc.77(3) (2008), 441–453] proved that

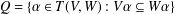$$\begin{eqnarray}\displaystyle Q=\{\unicode[STIX]{x1D6FC}\in T(V,W):V\unicode[STIX]{x1D6FC}\subseteq W\unicode[STIX]{x1D6FC}\} & & \displaystyle \nonumber\end{eqnarray}$$
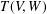is the largest regular subsemigroup of $T(V,W)$ and characterized Green’s relations on 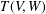$T(V,W)$. In this paper, we determine all the maximal regular subsemigroups of 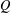$Q$ when 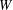$W$ is a finite-dimensional subspace of 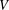$V$ over a finite field. Moreover, we compute the rank and idempotent rank of 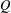$Q$ when 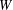$W$ is an $n$-dimensional subspace of an 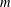$m$-dimensional vector space 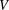$V$ over a finite field 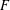$F$.

Keywords

linear transformationsregular subsemigroupsrankidempotent rank

MSC classification

Primary: 20M20: Semigroups of transformations, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 3 , December 2017 , pp. 402 - 419
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was supported by Chiang Mai University.

References

Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, Vol. I, Mathematical Surveys, 7 (American Mathematical Society, Providence, RI, 1961).Google Scholar
Fernandes, V. H. and Sanwong, J., ‘On the ranks of semigroups of transformations on a finite set with restricted range’, Algebra Colloq. 21(3) (2014), 497–510.Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory, London Mathematical Society Monographs. New Series, 12 (Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1995).Google Scholar
Mendes-Gonçalves, S. and Sullivan, R. P., ‘The ideal structure of semigroups of transformations with restricted range’, Bull. Aust. Math. Soc. 83(2) (2011), 289–300.Google Scholar
Nenthein, S. and Kemprasit, Y., ‘Regular elements of some semigroups of linear transformations and matrices’, Int. Math. Forum 2(1–4) (2007), 155–166.Google Scholar
Nenthein, S., Youngkhong, P. and Kemprasit, Y., ‘Regular elements of some transformation semigroups’, Pure Math. Appl. 16(3) (2005), 307–314.Google Scholar
Rotman, J. J., An Introduction to the Theory of Groups, 4th edn, Graduate Texts in Mathematics, 148 (Springer, New York, 1995).Google Scholar
Sanwong, J., ‘The regular part of a semigroup of transformations with restricted range’, Semigroup Forum 83(1) (2011), 134–146.Google Scholar
Sanwong, J. and Sommanee, W., ‘Regularity and Green’s relations on a semigroup of transformations with restricted range’, Int. J. Math. Math. Sci. (2008), 794013, 11.Google Scholar
Sommanee, W. and Sanwong, J., ‘Rank and idempotent rank of finite full transformation semigroups with restricted range’, Semigroup Forum 87(1) (2013), 230–242.Google Scholar
Sullivan, R. P., ‘Semigroups of linear transformations with restricted range’, Bull. Aust. Math. Soc. 77(3) (2008), 441–453.Google Scholar
Symons, J. S. V., ‘Some results concerning a transformation semigroup’, J. Aust. Math. Soc. 19(4) (1975), 413–425.Google Scholar
Tingley, D., ‘Complements of linear subspaces’, Math. Mag. 64(2) (1991), 98–103.Google Scholar
Waterhouse, W. C., ‘Two generators for the general linear groups over finite fields’, Linear Multilinear Algebra 24(4) (1989), 227–230.Google Scholar
You, T., ‘Maximal regular subsemigroups of certain semigroups of transformations’, Semigroup Forum 64(3) (2002), 391–396.Google Scholar