Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-31T09:00:16.265Z Has data issue: false hasContentIssue false
  • English
  • Français

QUASI MULTIPLICATION AND 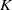$K$-GROUPS

Part of: Homological methods Grothendieck groups and $K_0$ Whitehead groups and $K_1$ Categories and geometry

Published online by Cambridge University Press:  28 February 2013

TSIU-KWEN LEE  and
ALBERT JEU-LIANG SHEU
TSIU-KWEN LEE
Affiliation:
Department of Mathematics, National Taiwan University, Taipei, Taiwan email tklee@math.ntu.edu.tw
ALBERT JEU-LIANG SHEU*
Affiliation:
Department of Mathematics, University of Kansas, Lawrence, KS 66045, USA
*
✉sheu@math.ku.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a negative answer to the question raised by Mart Abel about whether his proposed definition of 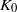${K}_{0} $ and 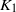${K}_{1} $ groups in terms of quasi multiplication is indeed equivalent to the established ones in algebraic 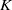$K$-theory.

Keywords

K0-groupK1-groupquasi multiplicationquasi invertibilityGrothendieck groupJacobson radicalalgebraic K-theorytopological K-theory

MSC classification

Secondary: 16E20: Grothendieck groups, $K$-theory, etc. 18F30: Grothendieck groups 19A99: None of the above, but in this section 19B99: None of the above, but in this section

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 2 , April 2013 , pp. 257 - 267
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Abel, M., ‘On algebraic $K$-theory’, International Conference on Topological Algebras and their Applications (ICTAA) Tartu, 24–27 January 2008, Mathematics Studies, 4 (Estonian Mathematical Society, Tartu, Estonia, 2008), pp. 7–12.Google Scholar
Husemoller, D., Fibre Bundles (McGraw-Hill, New York, 1966).CrossRefGoogle Scholar
Lang, S., Algebra (Addison-Wesley, Reading, MA, 1965).Google Scholar
Palmer, T. W., Banach Algebras and the General Theory of *-Algebras, Vol. I (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar
Swan, R. W., ‘Vector bundles and projective modules’, Trans. Amer. Math. Soc. 705 (1962), 264–277.CrossRefGoogle Scholar
Taylor, J., ‘Banach algebras and topology’, in: Algebras in Analysis (Academic Press, New York, 1975).Google Scholar
Weibel, C. A., The K-book: An Introduction to Algebraic K-theory, 2012,http://www.math.rutgers.edu/~weibel/Kbook.html.Google Scholar