Article contents
The product of independent random variables with slowly varying truncated moments
Published online by Cambridge University Press: 09 April 2009
Abstract
The Mellin-Stieltjes convolution and related decomposition of distributions in M(α) (the class of distributions μ on (0, ∞) with slowly varying αth truncated moments 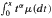 ) are investigated. Maller shows that if X and Y are independent non-negative random variables with distributions μ and v, respectively, and both μ and v are in D2, the domain attraction of Gaussian distribution, then the distribution of the product XY (that is, the Mellin-Stieltjes convolution μ ^ v of μ and v) also belongs to it. He conjectures that, conversely, if μ ∘ v belongs to D2, then both μ and v are in it. It is shown that this conjecture is not true: there exist distributions μ ∈ D2 and v μ ∈ D2 such that μ ^ v belongs to D2. Some subclasses of D2 are given with the property that if μ ^ v belongs to it, then both μ and v are in D2.
) are investigated. Maller shows that if X and Y are independent non-negative random variables with distributions μ and v, respectively, and both μ and v are in D2, the domain attraction of Gaussian distribution, then the distribution of the product XY (that is, the Mellin-Stieltjes convolution μ ^ v of μ and v) also belongs to it. He conjectures that, conversely, if μ ∘ v belongs to D2, then both μ and v are in it. It is shown that this conjecture is not true: there exist distributions μ ∈ D2 and v μ ∈ D2 such that μ ^ v belongs to D2. Some subclasses of D2 are given with the property that if μ ^ v belongs to it, then both μ and v are in D2.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1997
References
- 4
- Cited by

