Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chmieliński, Jacek
2014.
Normed spaces equivalent to inner product spaces and stability of functional equations.
Aequationes mathematicae,
Vol. 87,
Issue. 1-2,
p.
147.
Ikeda, Toshiharu
and
Kato, Mikio
2014.
Notes on von Neumann–Jordan and James Constants for Absolute Norms on $${\mathbb{R}^2}$$ R 2.
Mediterranean Journal of Mathematics,
Vol. 11,
Issue. 2,
p.
633.
Passer, Benjamin
2015.
An approximate version of the Jordan von Neumann theorem for finite-dimensional real normed spaces.
Linear and Multilinear Algebra,
Vol. 63,
Issue. 1,
p.
68.

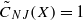 that is not isomorphic to any Hilbert space, where
that is not isomorphic to any Hilbert space, where 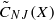 denotes the infimum of all von Neumann–Jordan constants for equivalent norms of
denotes the infimum of all von Neumann–Jordan constants for equivalent norms of 