No CrossRef data available.
Article contents
ON THE UMBILICITY OF HYPERSURFACES IN THE HYPERBOLIC SPACE
Published online by Cambridge University Press: 16 November 2016
Abstract
In this paper, we establish new characterization results concerning totally umbilical hypersurfaces of the hyperbolic space 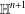 $\mathbb{H}^{n+1}$ , under suitable constraints on the behavior of the Lorentzian Gauss map of complete hypersurfaces having some constant higher order mean curvature. Furthermore, working with different warped product models for
$\mathbb{H}^{n+1}$ , under suitable constraints on the behavior of the Lorentzian Gauss map of complete hypersurfaces having some constant higher order mean curvature. Furthermore, working with different warped product models for 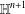 $\mathbb{H}^{n+1}$ and supposing that certain natural inequalities involving two consecutive higher order mean curvature functions are satisfied, we study the rigidity and the nonexistence of complete hypersurfaces immersed in
$\mathbb{H}^{n+1}$ and supposing that certain natural inequalities involving two consecutive higher order mean curvature functions are satisfied, we study the rigidity and the nonexistence of complete hypersurfaces immersed in 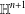 $\mathbb{H}^{n+1}$ .
$\mathbb{H}^{n+1}$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
Footnotes
The first author is partially supported by CNPq, Brazil, grant number 302738/2014-2. The second author is partially supported by CNPq, Brazil, grant number 456755/2014-4. The third author is partially supported by CNPq, Brazil, grant number 303977/2015-9.

